题目内容
3.已知椭圆焦点F(0,c)与短轴的两个端点连线互相垂直,且焦距为2.(1)求椭圆的标准方程;
(2)点C在直线l:y=x+2$\sqrt{2}$上,直线l′∥l,且与椭圆交于A,B两点,当△ABC是等边三角形时,求直线l′的方程.
分析 (1)作椭圆的图象,从而可得b=c=1,a=$\sqrt{2}$;
(2)由题意作图象,设直线l′的方程为y=x+b,从而联立可得$\left\{\begin{array}{l}{y=x+b}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,化简可得3x2+4bx+2b2-2=0,设A(x1,y1),B(x2,y2),从而可得(x1-x2)2=$\frac{24-8{b}^{2}}{9}$,而l与l′的距离d=$\frac{|b-2\sqrt{2}|}{\sqrt{2}}$,由题意得d=$\frac{\sqrt{3}}{2}$|AB|,从而解得.
解答 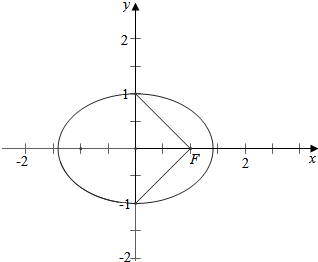 解:(1)作椭圆的图象如右图,
解:(1)作椭圆的图象如右图,
结合图象及题意可得,
b=c=1,a=$\sqrt{2}$;
故椭圆的标准方程为$\frac{{x}^{2}}{2}$+y2=1;
(2)由题意作图如右图,
设直线l′的方程为y=x+b,
联立可得,$\left\{\begin{array}{l}{y=x+b}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,
消y得,3x2+4bx+2b2-2=0,
设A(x1,y1),B(x2,y2),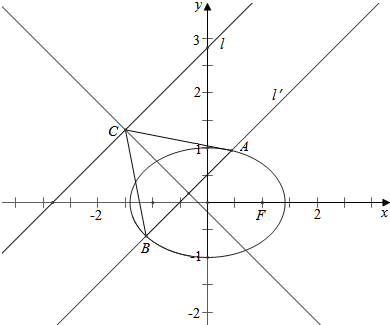
则x1+x2=-$\frac{4b}{3}$,x1x2=$\frac{1}{3}$(2b2-2);
则(x1-x2)2=(x1+x2)2-4x1x2
=(-$\frac{4b}{3}$)2-4×$\frac{1}{3}$(2b2-2)
=$\frac{24-8{b}^{2}}{9}$,
l与l′的距离d=$\frac{|b-2\sqrt{2}|}{\sqrt{2}}$,
∵d=$\frac{\sqrt{3}}{2}$|AB|,
∴2$\frac{|b-2\sqrt{2}|}{\sqrt{2}}$=$\sqrt{3}$•$\sqrt{2}$•|x1-x2|,
即|b-2$\sqrt{2}$|=$\sqrt{3}$•|x1-x2|,
故(b-2$\sqrt{2}$)2=3•$\frac{24-8{b}^{2}}{9}$,
解得,b=0或b=$\frac{12\sqrt{2}}{11}$;
故直线l′的方程为y=x或y=x+$\frac{12\sqrt{2}}{11}$.
点评 本题考查了数形结合的思想应用及直线与椭圆的位置关系的判断与应用.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
| A. | $\frac{2}{3}<m<\frac{11}{8}$ | B. | $m<\frac{11}{8}$ | C. | $m>\frac{2}{3}$ | D. | $m<\frac{2}{3}$或$m>\frac{11}{8}$ |
| A. | (-π,-$\frac{3π}{4}$) | B. | (-$\frac{3π}{4}$,0) | C. | (-$\frac{π}{4}$,$\frac{π}{4}$) | D. | ($\frac{π}{2}$,$\frac{3π}{2}$) |
| A. | (0,1) | B. | (0,±2) | C. | (±1,0) | D. | (±2,0) |
| A. | 一点 | B. | 两点 | C. | 一条抛物线 | D. | 两条抛物线 |