题目内容
12.已知椭圆C:x2+$\frac{{y}^{2}}{15}$=1,过C任意一点M作与直线l0:x+y-6=0夹角为30°的直线l,l交l0于点P,则|MP|的最小值是2$\sqrt{2}$.分析 利用曲线C的参数方程求出点P到直线l的距离d,计算|MP|=$\frac{d}{si{n30}^{°}}$,利用直线和椭圆相切的条件进行求解即可.
解答 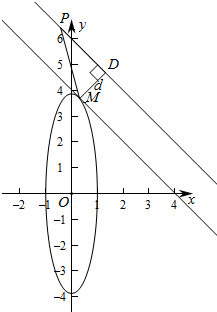 解:∵过C任意一点M作与直线l0:x+y-6=0夹角为30°的直线l,l交l0于点P,
解:∵过C任意一点M作与直线l0:x+y-6=0夹角为30°的直线l,l交l0于点P,
∴|MP|=$\frac{d}{si{n30}^{°}}$=2d,
即要使|MP|最小,则只需要M到直线x+y-6=0的距离最小即可,
设与x+y-6=0平行且与椭圆相切的直线为x+y+c=0,
即x=-(y+c),代入x2+$\frac{{y}^{2}}{15}$=1得(y+c)2+$\frac{{y}^{2}}{15}$=1,
整理得$\frac{16}{15}$y2+2cy+c2-1=0,
由判别式△=0得△=4c2-4×$\frac{16}{15}$(c2-1)=0.
即c2=16,得c=±4,
即切线为x+y+4=0(舍)或x+y-4=0,
则x+y-4=0到x+y-6=0的距离d=$\frac{|-4+6|}{\sqrt{2}}=\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
即d=$\sqrt{2}$,
则|MP|的最小值为|MP|=2d=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$
点评 本题考查了直线与椭圆的位置关系的应用,利用直线和椭圆相切以及平行直线的距离公式是解决本题的关键.

练习册系列答案
相关题目
2.已知向量$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(2m,1),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则m的值为( )
| A. | -1 | B. | 1 | C. | $-\frac{1}{4}$ | D. | $\frac{1}{4}$ |
17.在三棱锥P-ABC中,PA⊥平面ABC,且AB⊥BC,AB=$\sqrt{6}$,PA=BC=$\sqrt{5}$,则三棱锥P-ABC的表面积为( )
| A. | 12π | B. | 16π | C. | 18π | D. | 24π |
1.Sn是数列{an}的前n项和log2Sn=n(n=1,2,3,…),那么数列{an}( )
| A. | 是公比为2的等比数列 | B. | 是公差为2的等差数列 | ||
| C. | 是公比为$\frac{1}{2}$的等比数列 | D. | 既非等差数列又非等比数列 |