Question

15．一动圆与圆（x-2）²+y²=1及y轴都相切．则动圆圆心的轨迹是（　　）

• A． 一点
• B． 两点
• C． 一条抛物线
• D． 两条抛物线

Answer 1

分析 根据圆与圆的位置关系，结合抛物线的定义进行求解即可．

解答 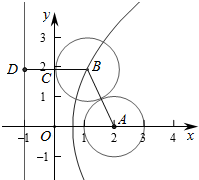解：设动圆圆心为B（x，y），动圆的半径为R，
则圆（x-2）²+y²=1的圆心A（2，0），半径为1，
①若动圆与圆（x-2）²+y²=1外切及y轴相切．
则|AB|=R+1，且|BC|=R，
作直线x=-1，则B到直线x=-1距离为|BD|=R+1，
即|AB|=|BD|，
即B到直线x=-1和定点A（2，0）的距离相等，
则动圆圆心的轨迹是以A为焦点，x=-1为准线的抛物线，
②若动圆与圆（x-2）²+y²=1内切及y轴相切．
则|AB|=R-1，且|BD|=R，
作直线x=1，则B到直线x=1距离为|BC|=R-1，
即|AB|=|BC|，
即B到直线x=1和定点A（2，0）的距离相等，
则动圆圆心的轨迹是以A为焦点，x=1为准线的抛物线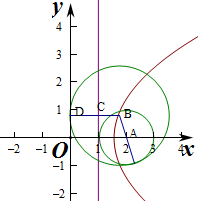
，
故动圆圆心的轨迹是两条抛物线，
故选：D．

点评 本题主要考查动点轨迹的判断，结合圆与圆的位置关系，利用抛物线的定义是解决本题的关键．