题目内容
设a、b是互不相等的正数，则下列不等式中恒成立的个数是（ ）
①（a+3）2＞2a2+6a+11
②
-
≤
-
③a2+
≥a+
．
①（a+3）2＞2a2+6a+11
②
| a+3 |
| a+1 |
| a+2 |
| a |
③a2+
| 1 |
| a2 |
| 1 |
| a |
| A、0 | B、1 | C、2 | D、3 |
考点：基本不等式
专题：不等式的解法及应用
分析：①③用作差法比较大小，②用放缩法比较大小．
解答：
解：①（a+3）2-（2a2+6a+11）=a2+6a+9-2a2-6a-11=-a2-2＜0，故不成立．
②
-
=
＜
≤
-
，故成立．
③a2+
-a-
=
（a4+1-a3-a）=
（a4+1-a3-a）=
≥0，故成立．
故下列不等式中恒成立的个数是2个．
故选：C．
②
| a+3 |
| a+1 |
| 2 | ||||
|
| 2 | ||||
|
| a+2 |
| a |
③a2+
| 1 |
| a2 |
| 1 |
| a |
| 1 |
| a2 |
| 1 |
| a2 |
| (a-1)2(a2+a+1) |
| a2 |
故下列不等式中恒成立的个数是2个．
故选：C．
点评：本题主要考查了不等式比较大小，常用作差法比较大小，放缩法证明不等式等．
练习册系列答案
相关题目
定义域为R的函数f（x）的图象关于直线x=1对称，当x∈[0，1]时，f（x）=x，且对任意x∈R都有f（x+2）=f（x），g（x）=
，则函数F（x）=g（x）-
x的零点个数为（ ）
|
| 1 |
| 2014 |
| A、1008 | B、2013 |
| C、2014 | D、2015 |
过正三棱锥的侧棱与底面中心作截面，如果截面是等腰三角形，则侧面与底面所成角的余弦值是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
若向量
=（1，3），
=（x，-1）的夹角为钝角，则实数x的取值范围为（ ）
| a |
| b |
| A、（-∞，3） | ||||
| B、（3，+∞） | ||||
C、（-∞，
| ||||
D、（-∞，-
|
| ∫ |
0 |
A、-
| ||||
B、
| ||||
C、
| ||||
| D、1 |
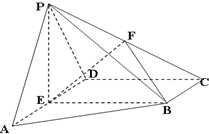已知在四棱锥P-ABCD中，AD∥BC，AD⊥CD，PA=PD=AD=2BC=2CD，E，F分别是AD，PC的中点．
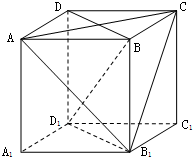如图，正方体ABCD-A1B1C1D1是棱长为1的正方体．