题目内容
巳知函数f(x)=x2-2ax-2alnx,g(x)=ln2x+2a2,其中x>0,a∈R.
(Ⅰ)若x=1是函数f(x)的极值点,求a的值;
(Ⅱ)若f(x)在区间(2,+∞)上单调递增,求a的取值范围;
(Ⅲ)记F(x)=f(x)+g(x),求证:F(x)≥
.
(Ⅰ)若x=1是函数f(x)的极值点,求a的值;
(Ⅱ)若f(x)在区间(2,+∞)上单调递增,求a的取值范围;
(Ⅲ)记F(x)=f(x)+g(x),求证:F(x)≥
| 1 |
| 2 |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)根据极点的定义很容易求出a的值,由于只是导函数在一点的导数等于0,不能说明这一点是极点,所以求出a之后需验证它是否是极点.
(Ⅱ)由f(x)在区间(2,+∞)上单调递增,便得到在该区间上f′(x)≥0,然后用x表示a,即得到a≤
,只需求
的范围即可.
(Ⅲ)求出F(x)=x2-2ax-2alnx+ln2x+2a2,通过观察F(x)的解析式的形式,能够想到解析式里可能存在完全平方式,所以试着构造完全平方式,结果能构造出完全平方式,并得到:F(x)=2(a-
)2+
≥
,所以只要x-lnx≥1即可,这点的说明,利用求导数,根据单调性判断即可.
(Ⅱ)由f(x)在区间(2,+∞)上单调递增,便得到在该区间上f′(x)≥0,然后用x表示a,即得到a≤
| x2 |
| x+1 |
| x2 |
| x+1 |
(Ⅲ)求出F(x)=x2-2ax-2alnx+ln2x+2a2,通过观察F(x)的解析式的形式,能够想到解析式里可能存在完全平方式,所以试着构造完全平方式,结果能构造出完全平方式,并得到:F(x)=2(a-
| x+lnx |
| 2 |
| (x-lnx)2 |
| 2 |
| (x-lnx)2 |
| 2 |
解答:
解:(Ⅰ)f′(x)=2x-2a-
=
(x>0);
∵x=1是函数f(x)的极值点;
∴f′(1)=2-2a-2a=0,解得a=
;
经检验x=1为函数f(x)的极值点,所以a=
.
(II)∵f(x)在区间(2,+∞)上单调递增;
∴f′(x)=
≥0在区间(2,+∞)上恒成立;
∴a≤
对区间(2,+∞)恒成立;
令M(x)=
,则M′(x)=
=
;
当x∈(2,+∞)时,M′(x)>0,有M(x)=
>M(2)=
;
∴a的取值范围为(-∞,
].
(Ⅲ)F(x)=x2-2ax-2alnx+ln2x+2a2=2[a2-(x+lnx)a+
];
令P(a)=a2-(x+lnx)a+
;
则P(a)=(a-
)2-(
)2+
=(a-
)2+
≥
;
令Q(x)=x-lnx,则Q′(x)=1-
=
;
显然Q(x)在(0,1]上单调递减,在(1,+∞)上单调递增;
则Q(x)min=Q(1)=1,则P(a)≥
;
故F(x)≥2×
=
.
| 2a |
| x |
| 2x2-2ax-2a |
| x |
∵x=1是函数f(x)的极值点;
∴f′(1)=2-2a-2a=0,解得a=
| 1 |
| 2 |
经检验x=1为函数f(x)的极值点,所以a=
| 1 |
| 2 |
(II)∵f(x)在区间(2,+∞)上单调递增;
∴f′(x)=
| 2x2-2ax-2a |
| x |
∴a≤
| x2 |
| x+1 |
令M(x)=
| x2 |
| x+1 |
| 2x(x+1)-x2 |
| (x+1)2 |
| x2+2x |
| (x+1)2 |
当x∈(2,+∞)时,M′(x)>0,有M(x)=
| x2 |
| x+1 |
| 4 |
| 3 |
∴a的取值范围为(-∞,
| 4 |
| 3 |
(Ⅲ)F(x)=x2-2ax-2alnx+ln2x+2a2=2[a2-(x+lnx)a+
| x2+ln2x |
| 2 |
令P(a)=a2-(x+lnx)a+
| x2+ln2x |
| 2 |
则P(a)=(a-
| x+lnx |
| 2 |
| x+lnx |
| 2 |
| x2+ln2x |
| 2 |
| x+lnx |
| 2 |
| (x-lnx)2 |
| 4 |
| (x-lnx)2 |
| 4 |
令Q(x)=x-lnx,则Q′(x)=1-
| 1 |
| x |
| x-1 |
| x |
显然Q(x)在(0,1]上单调递减,在(1,+∞)上单调递增;
则Q(x)min=Q(1)=1,则P(a)≥
| 1 |
| 4 |
故F(x)≥2×
| 1 |
| 4 |
| 1 |
| 2 |
点评:第一问中的a是比较容易求出的,然而需验证求的a符合题意,这需要理解极值的定义.第二问是根据函数导数符号与函数单调性的关系去求解的,而比较关键的是得到a≤
.第三问的关键是构造完全平方式,使一个完全平方式里含a,另一个不含a,因为a的值不确定,并且要证的不等式的右边不含a.
| x2 |
| x+1 |

练习册系列答案
相关题目
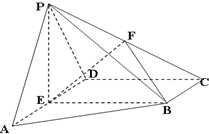 已知在四棱锥P-ABCD中,AD∥BC,AD⊥CD,PA=PD=AD=2BC=2CD,E,F分别是AD,PC的中点.
已知在四棱锥P-ABCD中,AD∥BC,AD⊥CD,PA=PD=AD=2BC=2CD,E,F分别是AD,PC的中点.