题目内容
设矩阵A=
,若存在一矩阵P=
使得A=PBP-1.试求:
(Ⅰ)矩阵B;
(Ⅱ)B3.
|
|
(Ⅰ)矩阵B;
(Ⅱ)B3.
考点:变换、矩阵的相等
专题:矩阵和变换
分析:(Ⅰ)设矩阵B=
,则由A=PBP-1,可得AP=PB,利用矩阵乘法,列出方程组,求出a、b、c、d 的值,即可求出矩阵B;
(Ⅱ)首先根据矩阵的乘法,求出B2,然后再和矩阵B相乘,求出B3即可.
|
(Ⅱ)首先根据矩阵的乘法,求出B2,然后再和矩阵B相乘,求出B3即可.
解答:
解:(Ⅰ)设矩阵B=
,则由A=PBP-1,可得AP=PB,
即
=
,
整理得
,
解得a=2,b=0,c=0,d=3,
即B=
;
(Ⅱ)由(1)知B2=
=
,
所以B3=B2B=
=
.
|
即
|
|
|
|
整理得
|
解得a=2,b=0,c=0,d=3,
即B=
|
(Ⅱ)由(1)知B2=
|
|
|
所以B3=B2B=
|
|
|
点评:本题主要考查矩阵的运算等基础知识,考查学生的运算求解能力,考查化归与转化思想的运用,属于基础题.

练习册系列答案
相关题目
过点P(-2,1)且方向向量为
=(-2,3)的直线方程为( )
| n |
| A、3x+2y-8=0 |
| B、3x+2y+4=0 |
| C、2x+3y+1=0 |
| D、2x+3y-7=0 |
| ∫ |
0 |
A、-
| ||||
B、
| ||||
C、
| ||||
| D、1 |
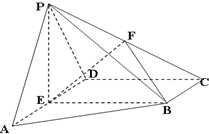 已知在四棱锥P-ABCD中,AD∥BC,AD⊥CD,PA=PD=AD=2BC=2CD,E,F分别是AD,PC的中点.
已知在四棱锥P-ABCD中,AD∥BC,AD⊥CD,PA=PD=AD=2BC=2CD,E,F分别是AD,PC的中点.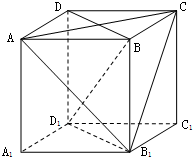 如图,正方体ABCD-A1B1C1D1是棱长为1的正方体.
如图,正方体ABCD-A1B1C1D1是棱长为1的正方体.