题目内容
已知向量
，
满足
•
=0，|
|=1，|
|=2，则|
-
|=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、0 | ||
| B、1 | ||
| C、2 | ||
D、
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用数量积的性质即可得出．
解答：
解：∵向量
，
满足
•
=0，|
|=1，|
|=2，
∴|
-
|=
=
=
．
故选：D．
| a |
| b |
| a |
| b |
| a |
| b |
∴|
| a |
| b |
|
| 1+22-0 |
| 5 |
故选：D．
点评：本题考查了数量积的性质，属于基础题．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
椭圆
+
=1的焦点为F1，F2，P为椭圆上的点，已知∠F1PF2=90°，则△PF1F2的面积为（ ）
| x2 |
| 25 |
| y2 |
| 9 |
| A、9 | B、12 |
| C、18 | D、以上均不对 |
定义域为R的函数f（x）的图象关于直线x=1对称，当x∈[0，1]时，f（x）=x，且对任意x∈R都有f（x+2）=f（x），g（x）=
，则函数F（x）=g（x）-
x的零点个数为（ ）
|
| 1 |
| 2014 |
| A、1008 | B、2013 |
| C、2014 | D、2015 |
某学校实行改革，每天上午改为上五节课，40分钟一节，其中高二（12）班周二上午安排数学、物理、生物、语文、体育五节课，若体育课不排第一节，数学课与物理课不相邻的排法总数为（ ）
| A、48 | B、60 | C、72 | D、96 |
若
=（3，m），
=（2，-1），且
⊥
，则实数m的值为（ ）
| a |
| b |
| a |
| b |
| A、3 | B、6 | C、-3 | D、-6 |
过点P（-2，1）且方向向量为
=（-2，3）的直线方程为（ ）
| n |
| A、3x+2y-8=0 |
| B、3x+2y+4=0 |
| C、2x+3y+1=0 |
| D、2x+3y-7=0 |
过正三棱锥的侧棱与底面中心作截面，如果截面是等腰三角形，则侧面与底面所成角的余弦值是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
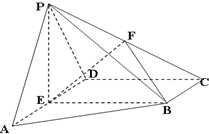已知在四棱锥P-ABCD中，AD∥BC，AD⊥CD，PA=PD=AD=2BC=2CD，E，F分别是AD，PC的中点．