题目内容
根据下边给出的数塔猜测123456×9+8=( )
1×9+2=11
12×9+3=111
123×9+4=1111
1234×9+5=11111.
1×9+2=11
12×9+3=111
123×9+4=1111
1234×9+5=11111.
| A、1111110 |
| B、1111111 |
| C、1111112 |
| D、1111113 |
考点:归纳推理
专题:计算题,推理和证明
分析:分析已知中的数塔,可知,等式右边各数位上的数字均为1,位数跟等式左边的第二个加数相同,进而得到答案.
解答:
解:由1×9+2=11;
12×9+3=111;
123×9+4=1111;
1234×9+5=11111;
…
归纳可得:等式右边各数位上的数字均为1,位数跟等式左边的第二个加数相同,
∴123456×9+7=1111111,∴123456×9+8=1111112,
故选:C.
12×9+3=111;
123×9+4=1111;
1234×9+5=11111;
…
归纳可得:等式右边各数位上的数字均为1,位数跟等式左边的第二个加数相同,
∴123456×9+7=1111111,∴123456×9+8=1111112,
故选:C.
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
若(x+
)n展开式中只有第6项的系数最大,则常数项是( )
| 1 |
| x |
| A、第5项 | B、第6项 |
| C、第7项 | D、第8项 |
已知向量
与
的夹角为为30°,且|
|=
,|
|=2,则|
+
|=( )
| a |
| b |
| a |
| 3 |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)的定义域为R,其导函数f′(x)的图象如图所示,则函数f(x)( )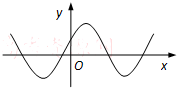

| A、有三个极值点,但无法判断有几个极大值,几个极小值 |
| B、有一个极大值点,两个极小值点 |
| C、有两个极大值点,两个极小值点 |
| D、有四个极值点,但无法判断有几个极大值,几个极小值 |
已知实数a,b∈{1,2,3},则函数y=
x3-ax2+bx+5有极值的概率为( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
共轭的两个复数之和大于2的一个充要条件为( )
| A、两复数的实部都大于1 |
| B、两复数的实部都大于2 |
| C、两复数的虚部都大于1 |
| D、两复数的虚部都大于2 |
已知函数f(x)=2ln3x+8x,则
的值为( )
| lim |
| △x→0 |
| f(1+2△x)-f(1) |
| △x |
| A、-20 | B、-10 |
| C、10 | D、20 |
若函数y=x2-3x-4的定义域为[0,m],值域为[-
,-4],则m的取值范围是( )
| 25 |
| 4 |
| A、(0,4] | ||
B、[
| ||
C、[
| ||
D、[
|