题目内容
 如图,在四棱锥S-ABCD中,SD⊥底面ABCD,底面ABCD是矩形,且SD=AD=
如图,在四棱锥S-ABCD中,SD⊥底面ABCD,底面ABCD是矩形,且SD=AD=| 2 |
(1)求证:平面BED⊥平面SAB;
(2)求平面BED与平面SBC所成二面角(锐角)的大小.
考点:与二面角有关的立体几何综合题,平面与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明平面BED⊥平面SAB,利用面面垂直的判定定理,证明DE⊥平面SAB即可;
(2)建立空间直角坐标系,求出平面BED与平面SBC的法向量,利用向量的夹角公式,即可求平面BED与平面SBC所成二面角(锐角)的大小.
(2)建立空间直角坐标系,求出平面BED与平面SBC的法向量,利用向量的夹角公式,即可求平面BED与平面SBC所成二面角(锐角)的大小.
解答:
(1)证明:∵SD⊥底面ABCD,SD?平面SAD,
∴平面SAD⊥平面ABCD…(2分)
∵AB⊥AD,平面SAD∩平面ABCDAD,
∴AB⊥平面SAD,
又DE?平面SAD,
∴DE⊥AB,…(4分)
∵SD=AD,E是SA的中点,∴DE⊥SA,
∵AB∩SA=A,DE⊥AB,DE⊥SA,
∴DE⊥平面SAB,
∵DE?平面BED,
∴平面BED⊥平面SAB.…(6分)
(2)解:由题意知SD,AD,DC两两垂直,建立如图所示的空间直角坐标系D-xyz,不妨设AD=2.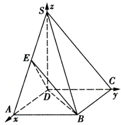
则D(0,0,0),A(2,0,0),B(2,
,0),C(0,
,0),S(0,0,2),E(1,0,1),
∴
=(2,
,0),
=(1,0,1),
=(2,0,0),
=(0,-
,2)…(8分)
设
=(x1,y1,z1)是平面BED的法向量,则
,即
,
令x1=-1,则y1=
,z1=1,
∴
=(-1,
,1)是平面BED的一个法向量.
设
=(x2,y2,z2)是平面SBC的法向量,则
,即
,
解得x2=0,令y2=
,则z2=1,
∴
=(0,
,1)是平面SBC的一个法向量.…(10分)
∵cos?
,
>=
=
=
,
∴平面BED与平面SBC所成锐二面角的大小为
.…(12分)
∴平面SAD⊥平面ABCD…(2分)
∵AB⊥AD,平面SAD∩平面ABCDAD,
∴AB⊥平面SAD,
又DE?平面SAD,
∴DE⊥AB,…(4分)
∵SD=AD,E是SA的中点,∴DE⊥SA,
∵AB∩SA=A,DE⊥AB,DE⊥SA,
∴DE⊥平面SAB,
∵DE?平面BED,
∴平面BED⊥平面SAB.…(6分)
(2)解:由题意知SD,AD,DC两两垂直,建立如图所示的空间直角坐标系D-xyz,不妨设AD=2.

则D(0,0,0),A(2,0,0),B(2,
| 2 |
| 2 |
∴
| DB |
| 2 |
| DE |
| CB |
| CS |
| 2 |
设
| m |
|
|
令x1=-1,则y1=
| 2 |
∴
| m |
| 2 |
设
| n |
|
|
解得x2=0,令y2=
| 2 |
∴
| n |
| 2 |
∵cos?
| m |
| n |
| ||||
|
|
| 3 | ||
2
|
| ||
| 2 |
∴平面BED与平面SBC所成锐二面角的大小为
| π |
| 6 |
点评:本题考查面面垂直,考查面面角,解题的关键是掌握面面垂直的判定,正确利用向量法,属于中档题.

练习册系列答案
相关题目
如图,在△ABC中,AB=AC=BC=2,则
•
=( )

| AB |
| BC |

| A、1 | B、-1 | C、2 | D、-2 |
 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB= 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=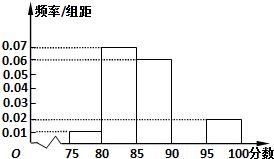 某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.