题目内容
已知函数f(x)=
是奇函数.
(1)求实数a的值;
(2)判断函数f(x)在R上的单调性,并给出证明过程;
(3)若函数f(x)的图象经过点(-1,-
),这对任意x∈R不等式f(x2-2mx+m+1)≤
恒成立,求实数m的范围.
| 1+a•2x |
| 2x+1 |
(1)求实数a的值;
(2)判断函数f(x)在R上的单调性,并给出证明过程;
(3)若函数f(x)的图象经过点(-1,-
| 1 |
| 3 |
| 1 |
| 3 |
考点:函数恒成立问题,函数单调性的判断与证明
专题:综合题,函数的性质及应用
分析:(1)利用f(0)=0可求得实数a的值;
(2)f(x)=-1+
为R上的减函数,利用导数法,易证f′(x)=-
<0,从而可使结论得证;
(3)依题意知f(-1)=
,f(x)=
为R上的减函数,?x∈R,f(x2-2mx+m+1)≤
=f(-1)恒成立?x2-2mx+m+2≥0恒成立?△≤0,从而可得实数m的范围.
(2)f(x)=-1+
| 2 |
| 2x+1 |
| 2x+1ln2 |
| (2x+1)2 |
(3)依题意知f(-1)=
| 1 |
| 3 |
| 1-2x |
| 2x+1 |
| 1 |
| 3 |
解答:
解:(1)∵f(x)=
是R上的奇函数,
∴f(0)=
=0,
∴a=-1;
(2)由(1)知a=-1,
∴f(x)=
=-1+
,
∴f(x)=-1+
为R上的减函数;
证明如下:∵f(x)=-1+
,
∴f′(x)=-
<0,
∴f(x)=
为R上的减函数;
(3)∵函数f(x)的图象经过点(1,-
),即f(1)=-
,
∴f(-1)=-f(1)=
,
∴?x∈R,f(x2-2mx+m+1)≤
=f(-1)恒成立,由(2)知,f(x)=-1+
为R上的减函数,
∴x2-2mx+m+1≥-1恒成立,即x2-2mx+m+2≥0恒成立,
∴△=(-2m)2-4(m+2)≤0,
解得:-1≤m≤2.
∴实数m的范围为:[-1,2].
| 1+a•2x |
| 2x+1 |
∴f(0)=
| 1+a |
| 2 |
∴a=-1;
(2)由(1)知a=-1,
∴f(x)=
| 1-2x |
| 2x+1 |
| 2 |
| 2x+1 |
∴f(x)=-1+
| 2 |
| 2x+1 |
证明如下:∵f(x)=-1+
| 2 |
| 2x+1 |
∴f′(x)=-
| 2x+1ln2 |
| (2x+1)2 |
∴f(x)=
| 1-2x |
| 2x+1 |
(3)∵函数f(x)的图象经过点(1,-
| 1 |
| 3 |
| 1 |
| 3 |
∴f(-1)=-f(1)=
| 1 |
| 3 |
∴?x∈R,f(x2-2mx+m+1)≤
| 1 |
| 3 |
| 2 |
| 2x+1 |
∴x2-2mx+m+1≥-1恒成立,即x2-2mx+m+2≥0恒成立,
∴△=(-2m)2-4(m+2)≤0,
解得:-1≤m≤2.
∴实数m的范围为:[-1,2].
点评:本题考查函数恒成立问题,着重考查函数的单调性的判断与证明,考查等价转化思想与方程思想的综合运用,考查运算求解能力,属于难题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 如图,P为线段AB的垂直平分线上任意一点,O为平面内的任意一点,设
如图,P为线段AB的垂直平分线上任意一点,O为平面内的任意一点,设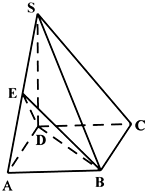 如图,在四棱锥S-ABCD中,SD⊥底面ABCD,底面ABCD是矩形,且
如图,在四棱锥S-ABCD中,SD⊥底面ABCD,底面ABCD是矩形,且 如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,四边形AA1C1C也为菱形且∠A1AC=∠DAB=60°,平面AA1C1C⊥平面ABCD.
如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,四边形AA1C1C也为菱形且∠A1AC=∠DAB=60°,平面AA1C1C⊥平面ABCD.