题目内容
如图，在△ABC中，AB=AC=BC=2，则
•
=（ ）
| AB |
| BC |
| A、1 | B、-1 | C、2 | D、-2 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量的数量积运算即可得出．
解答：
解：
•
=|
| |
|cos(π-
)=2×2×(-
)=-2．
故选：D．
| AB |
| BC |
| AB |
| BC |
| π |
| 3 |
| 1 |
| 2 |
故选：D．
点评：本题考查了向量的数量积运算，注意向量的夹角，属于基础题．
练习册系列答案
相关题目
设x=log52，y=e-
，z=
（e是自然对数的底数），则（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、x＜y＜z |
| B、y＜x＜z |
| C、z＜x＜y |
| D、x＜z＜y |
若对于任意的正数x，不等式3x（x2-2a）＞1恒成立，则a的取值范围是（ ）
| A、（-∞，+∞） | ||
| B、（-2，+∞） | ||
C、（
| ||
D、（-∞，-
|
已知A，B，C是单位圆O上任意的不同三点，若
=2
+x
，则正实数x的取值范围为（ ）
| OA |
| OB |
| OC |
| A、（0，2] |
| B、[1，3] |
| C、[2，4] |
| D、[3，5] |
m是一条直线，α，β是两个不同的平面，以下命题正确的是（ ）
| A、若m∥α，α∥β，则m∥β |
| B、若m∥α，m∥β，则α∥β |
| C、若m∥α，α⊥β，则m⊥β |
| D、若m∥α，m⊥β，则α⊥β |
如图，在直三棱柱ABC-A1B1C1（侧棱和底面垂直的棱柱）中，AB⊥BC，AB=BC=AA1=3，线段AC、A1B上分别有一点E、F，且满足2AE=EC，2BF=FA1．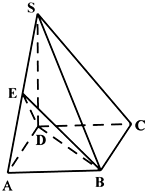
如图，在四棱锥S-ABCD中，SD⊥底面ABCD，底面ABCD是矩形，且