题目内容

已知函数f（x）=
ax+1+bx+1
ax+bx
，a＞0，b＞0，且a≠1，b≠1．
（1）判断函数f（x）的单调性；
（2）当a≠b时，利用（1）中的结论，证明不等式：
2
1
a
+
1
b
＜
ab
＜
a+b
2
＜
a2+b2
a+b
．
考点：指数函数综合题
专题：函数的性质及应用
分析：（1）分子分母同时除以bx，然后根据指数函数和分式函数的单调性之间的关系，即可判断函数f（x）的单调性；
（2）当a≠b时，利用（1）中的结论，将不等式中的式子转化为对应的函数值，利用函数的单调性即可证明不等式：
2
1
a
+
1
b
＜
ab
＜
a+b
2
＜
a2+b2
a+b
．
解答： 解：（1）f（x）=
ax+1+bx+1
ax+bx
=
a?(
a
b
)x+b
(
a
b
)x+1

=
a?[(
a
b
)x+1]+b-a
(
a
b
)x+1
=a+
b-a
(
a
b
)x+1
，
若a=b，则f（x）=a，此时函数为常数函数，不单调．
若a＞b，则b-a＜0，
a
b
＞1，
则y=(
a
b
)x+1为增函数，
∴根据 符合函数单调性之间的关系可知f（x）为增函数．
若a＜b，则b-a＞0，0＜
a
b
＜1，
则y=(
a
b
)x+1为减函数，
∴根据 符合函数单调性之间的关系可知f（x）为增函数．
综上当a≠b时，函数f（x）的单调递增．
（2）∵f（x）=
ax+1+bx+1
ax+bx
，
∴f（0）=
a+b
2
，f（1）=
a2+b2
a+b
，f（-1）=
2
1
a
+
1
b
，f（-
1
2
）=
ab
，
∵当a≠b时，函数f（x）的单调递增．且-1＜-
1
2
＜0＜1，
∴f（-1）＜f（-
1
2
）＜f（0）＜f（1），
即
2
1
a
+
1
b
＜
ab
＜
a+b
2
＜
a2+b2
a+b
成立．
点评：本题主要考查函数单调性的判断和应用，要求熟练掌握符合函数单调性之间的关系，将不等式中的式子转化为对应的函数值是解决本题的关键．
练习册系列答案
相关题目
若对于任意的正数x，不等式3x（x2-2a）＞1恒成立，则a的取值范围是（　　）
A、（-∞，+∞）
B、（-2，+∞）
C、（
1
2
，+∞）
D、（-∞，-
1
2
]
如图，在直三棱柱ABC-A1B1C1（侧棱和底面垂直的棱柱）中，AB⊥BC，AB=BC=AA1=3，线段AC、A1B上分别有一点E、F，且满足2AE=EC，2BF=FA1．
（1）求证：平面A1BC⊥侧面A1ABB1；
（2）求二面角F-BE-C的平面角的余弦值．
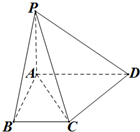如图，直角梯形ABCD中，∠ABC=∠BAD=90°，AB=BC=
1
2
AD．梯形ABCD所在平面外有一点P，满足PA⊥平面ABCD，PA=AB．
（1）求证：平面PCD⊥平面PAC；
（2）侧棱PA上是否存在点E，使得BE∥平面PCD？若存在，指出E的位置并证明；若不存在请说明理由；
【理】（3）求二面角A-PD-C的余弦值．
4个不同的玩具和3件不同的儿童服装排成一排，陈列在商店的柜台上，其中玩具与玩具放在一起，服装和服装放在一起，且某件服装不放在中间的排法有几种？
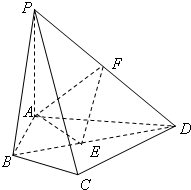如图，四棱锥P-ABCD中，PA⊥面ABCD，E、F分别为BD、PD的中点，EA=EB=AB=1，PA=2．
（Ⅰ）证明：PB∥面AEF；
（Ⅱ）求面PBD与面AEF所成锐角的余弦值．
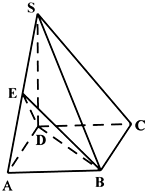如图，在四棱锥S-ABCD中，SD⊥底面ABCD，底面ABCD是矩形，且SD=AD=
2
AB，E是SA的中点．
（1）求证：平面BED⊥平面SAB；
（2）求平面BED与平面SBC所成二面角（锐角）的大小．
已知向量
p
=(cosα-5，-sinα)，
q
=(sinα-5，cosα)，
p
∥
q
，且α∈（0，π）．
（1）求tan2α的值；
（2）求2sin2(
α
2
+
π
6
)-sin(α+
π
6
)．
设
a
=(2cosωx，
3
)，
b
=(sinωx，cos2ωx-sin2ωx)（ω＞0），函数f(x)=
a
•
b
，且函数f（x）图象的一个对称中心与它相邻的一条对称轴之间的距离为
π
4
．
（Ⅰ）求函数f（x）的解析式．
（Ⅱ）在锐角三角形ABC中，角A、B、C的对边分别为a、b、c，且满足f（A）=0，B=
π
4
，a=2，求c边的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网