题目内容
已知函数f(x)=
,且关于x的方程f(x)+x+3a=0有两个实数根,则实数a的取值范围是 .
|
考点:根的存在性及根的个数判断
专题:数形结合,函数的性质及应用
分析:构造函数g(x)=f(x)+x,画出图象,转化为y=-3a与g(x)图象有两个交点,求解实数a的范围.
解答:
解:函数f(x)=
,令g(x)=f(x)+x作图象如下图
∵关于x的方程f(x)+x+3a=0有两个实数根,
∴y=-3a与g(x)图象有两个交点,
据图回答:-3a≤1,即a≥-
,
故答案为:[-
,+∞)

|
∵关于x的方程f(x)+x+3a=0有两个实数根,
∴y=-3a与g(x)图象有两个交点,
据图回答:-3a≤1,即a≥-
| 1 |
| 3 |
故答案为:[-
| 1 |
| 3 |

点评:本题考察了函数的图象与方程的关系,把方程根的问题,转化为函数图象的交点问题求解,结合图形求解.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
过点(-2,4)且在两坐标轴上截距的绝对值相等的直线有( )
| A、1条 | B、2条 | C、3条 | D、4条 |
 图是某赛季甲、乙两名篮球运动员每场比赛得分统计的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )
图是某赛季甲、乙两名篮球运动员每场比赛得分统计的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )| A、62 | B、63 | C、64 | D、65 |
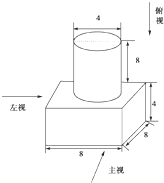 一几何体的直观图如图所示:
一几何体的直观图如图所示: