题目内容
若当x∈R时,y=
均有意义,则函数y=loga|
|的图象大致是( )
| 1-a|x| |
| 1 |
| x |
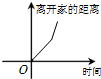
A、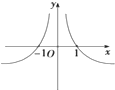 |
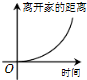
B、 |
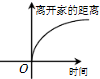
C、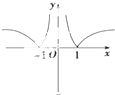 |
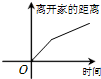
D、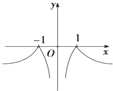 |
考点:函数的图象
专题:函数的性质及应用
分析:由对数函数的定义知a>0且a≠1,函数y=loga|
|的定义域为(-∞,0)∪(0,+∞)
由x∈A∪B={-4,-3,1}时,y=
均有意义,则
,推出0<a<1,再把函数表达式中的绝对值去掉,再讨论函数的单调性.
| 1 |
| x |
由x∈A∪B={-4,-3,1}时,y=
| 1-a|x| |
|
解答:
解:由对数函数的定义知a>0且a≠1,函数y=loga|
|的定义域为(-∞,0)∪(0,+∞)
若当x∈A∪B={-4,-3,1}时,y=
均有意义,则
,0<a<1,
又x>0时,y=loga
,
∵u=
单调递减,y=logau单调递减,∴由复合函数的单调性知y=loga
单调递增,
∵y=loga|
|=loga
为偶函数,其图象应关于y轴对称,∴x<0时,y=loga
单调递减,
综上知,选项B符合,
故选:B.
| 1 |
| x |
若当x∈A∪B={-4,-3,1}时,y=
| 1-a|x| |
|
又x>0时,y=loga
| 1 |
| x |
∵u=
| 1 |
| x |
| 1 |
| x |
∵y=loga|
| 1 |
| x |
| 1 |
| |x| |
| 1 |
| x |
综上知,选项B符合,
故选:B.
点评:本题主要考查函数的性质,利用函数的奇偶性判断函数的单调性,其中还应用了复合函数单调性的判断,较为综合.

练习册系列答案
相关题目
已知直线
=
+1与圆x2+y2=100有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有( )
| y |
| b |
| kx |
| b |
| A、60条 | B、66条 |
| C、70条 | D、71条 |
 已知函数f(x)=Asin(ωx+Φ)(A>0,ω>0,|Φ|<π)的部分图象如图所示.
已知函数f(x)=Asin(ωx+Φ)(A>0,ω>0,|Φ|<π)的部分图象如图所示.