题目内容
已知a＞0，b＞0，若直线l1：x+a2y+1=0与直线l2：（a2+1）x-by+3=0互相垂直，则ab的最小值是 ．
考点：直线的一般式方程与直线的垂直关系
专题：直线与圆
分析：根据两条直线垂直的性质求得ab关系，代入|ab|，利用基本不等式求得它的最小值．
解答：
解：由直线x+a2y+1=0与（a2+1）x-by+3=0互相垂直，
可得（a2+1）+a2（-b）=0，可得b=1+
，∵a＞0，b＞0，
∴|ab|=|a+
|=a+
≥2，
当且仅当a=1时取等号，
故|ab|的最小值为：2，
故答案为：2．
可得（a2+1）+a2（-b）=0，可得b=1+
| 1 |
| a2 |
∴|ab|=|a+
| 1 |
| a |
| 1 |
| a |
当且仅当a=1时取等号，
故|ab|的最小值为：2，
故答案为：2．
点评：本题主要考查两条直线垂直的性质，基本不等式的应用，属于基础题．
练习册系列答案
相关题目
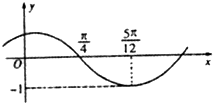从函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜| π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
定积分
xdx等于（ ）
| ∫ | 3 0 |
A、
| ||
| B、9 | ||
| C、8 | ||
| D、3 |