题目内容

18．在平行四边形ABCD中，若$|{\overrightarrow{AB}-\overrightarrow{AD}}|=|{\overrightarrow{AB}+\overrightarrow{AD}}|$，则平行四边形ABCD是（　　）
A．矩形B．梯形C．正方形D．菱形

分析 根据向量的基本运算，利用平方法进行判断即可．

解答 解：由$|{\overrightarrow{AB}-\overrightarrow{AD}}|=|{\overrightarrow{AB}+\overrightarrow{AD}}|$，平方得$\overrightarrow{AB}$2-2$\overrightarrow{AB}$•$\overrightarrow{AD}$+$\overrightarrow{AD}$2=$\overrightarrow{AB}$2+2$\overrightarrow{AB}$•$\overrightarrow{AD}$+$\overrightarrow{AD}$2，
得得$\overrightarrow{AB}$•$\overrightarrow{AD}$=0，即得$\overrightarrow{AB}$⊥$\overrightarrow{AD}$，
则平行四边形ABCD是矩形，
故选：A

点评 本题主要考查平行四边形的形状的判断，根据向量的基本运算，是解决本题的关键．

练习册系列答案
相关题目
8．已知椭圆$C：\frac{x^2}{3}+\frac{y^2}{2}=1$上的动点P与其顶点$A（-\sqrt{3}，0）$，$B（\sqrt{3}，0）$不重合．
（Ⅰ）求证：直线PA与PB的斜率乘积为定值；
（Ⅱ）设点M，N在椭圆C上，O为坐标原点，当OM∥PA，ON∥PB时，求△OMN的面积．
9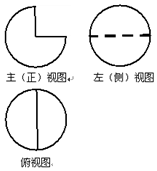．一个几何体的三视图如图所示，其中俯视图与左视图均为半径是1的圆，则这个几何体的体积是（　　）
A．$\frac{4π}{3}$B．$\frac{π}{3}$C．$\frac{2π}{3}$D．π
6．已知正项等比数列{an}中，Sn为其前n项和，a1=2，a2+a3=12，则S5=32．
13．椭圆C的焦点为F1（-$\sqrt{2}$，0），${F_2}（\sqrt{2}，0）$，且点$M（\sqrt{2}，1）$在椭圆C上．过点P（0，1）的动直线l与椭圆相交于A，B两点，点B关于y轴的对称点为点D（不同于点A）．
（I） 求椭圆C的标准方程；
（II）证明：直线AD恒过定点，并求出定点坐标．
3．已知数列{an}的前n项和为Sn，且${S_n}={n^2}+n$，则a3=6．
10．已知函数f（x）=lnx-mx（m＞0）．
（I） 若m=1，求曲线y=f（x）在点（1，f（1））处的切线方程；
（II）求函数f（x）的最大值g（m），并求使g（m）＞m-2成立的m取值范围．
7．已知函数$f（x）=\frac{lnx+1}{x}$．
（Ⅰ）求曲线y=f（x） 在函数f（x） 零点处的切线方程；
（Ⅱ）求函数y=f（x） 的单调区间；
（Ⅲ）若关于x 的方程f（x）=a 恰有两个不同的实根x1，x2，且x1＜x2，求证：${x_2}-{x_1}＞\frac{1}{a}-1$．
8．某四棱锥的三视图如图所示，该四棱锥的表面积是（　　）
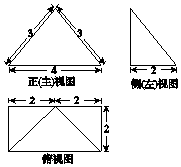
A．20+2$\sqrt{5}$B．14+4$\sqrt{5}$C．26D．12+2$\sqrt{5}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网