题目内容
4．已知向量$\vec a=（-1，\;1）$，$\vec b=（n，\;2）$，若$\vec a•\vec b=\frac{5}{3}$，则n=$\frac{1}{3}$．分析 利用向量积的坐标运算法则直接求解．
解答 解：∵向量$\vec a=（-1，\;1）$，$\vec b=（n，\;2）$，$\vec a•\vec b=\frac{5}{3}$，
∴$\overrightarrow{a}•\overrightarrow{b}$=-1+2=$\frac{5}{3}$，
解得n=$\frac{1}{3}$．
点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意向量坐标运算法则的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
14．下列说法错误的是（ ）
| A． | 命题“若x2-5x-6=0”则“x=2”的逆否命题是“若x≠2”则“x2-5x-6≠0” | |
| B． | 若命题p：存在${x_0}∈R，x_0^2+{x_0}+1＜0$，则￢p：对任意x∈R，x2+x+1≥0 | |
| C． | 若x，y∈R，则x=y是“$xy≥{（\frac{x+y}{2}）^2}$”的充要条件 | |
| D． | 已知命题p和q，若“p或q”为假命题，则命题p和q中必一真一假 |
19．对于任意的非零实数m，直线y=2x+m与双曲线$\frac{x^2}{a^2}-\frac{{{y^2}_{\;}}}{b^2}=1（{a＞0，b＞0}）$有且只有一个交点，则双曲线的离心率为（ ）
| A． | $\sqrt{5}$ | B． | $\frac{{\sqrt{5}}}{2}$ | C． | 2 | D． | $\sqrt{2}$ |
9．
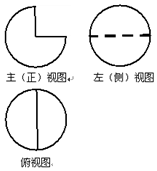一个几何体的三视图如图所示，其中俯视图与左视图均为半径是1的圆，则这个几何体的体积是（ ）
一个几何体的三视图如图所示，其中俯视图与左视图均为半径是1的圆，则这个几何体的体积是（ ）| A． | $\frac{4π}{3}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | π |
16．如果a＜b＜0，则下列不等式成立的是（ ）
| A． | $\frac{1}{a}＜\frac{1}{b}$ | B． | ac2＜bc2 | C． | a2＜b2 | D． | a3＜b3 |
