题目内容
20.已知函数f(x)=(sinx+cosx)2+2cos2x.(Ⅰ)求f(x)最小正周期;
(Ⅱ)求f(x)在区间[0,$\frac{π}{2}$]上的最大值和最小值.
分析 (Ⅰ)化函数f(x)为正弦型函数,即可求出f(x)的最小正周期;
(Ⅱ)由0≤x≤$\frac{π}{2}$求出2x+$\frac{π}{4}$的取值范围,再根据正弦函数的图象与性质即可求出f(x)的最值.
解答 解:(Ⅰ)f(x)=(sinx+cosx)2+2cos2x
=sin2x+2sinxcosx+cos2x+2cos2x
=1+sin2x+1+cos2x
=$\sqrt{2}$sin(2x+$\frac{π}{4}$)+2,…(4分)
所以f(x)的最小正周期为T=π;…(6分)
(Ⅱ)由0≤x≤$\frac{π}{2}$得,
0≤2x≤π,
所以$\frac{π}{4}$≤2 x+$\frac{π}{4}$≤$\frac{5π}{4}$;…(8分)
根据正弦函数y=sinx的图象可知
当$x=\frac{π}{8}$时,f(x)有最大值为2+$\sqrt{2}$,…(11分)
当$x=\frac{π}{2}$时,f(x)有最小值为1.…(13分)
点评 本题考查了三角函数的化简以及三角函数的图象与性质的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.某调查者从调查中获知某公司近年来科研费支出(xi) 用与公司所获得利润(yi)的统计资料如表:
科研费用支出(xi)与利润(yi)统计表 单位:万元
(1)由散点图可知,科研费用支出与利润线性相关,试根据以上数据求出y关于x的回归直线方程;
(2)当x=xi时,由回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$得到的函数值记为$\stackrel{∧}{{y}_{i}}$,我们将ε=|$\stackrel{∧}{{y}_{i}}$-yi|称为误差;
在表中6组数据中任取两组数据,求两组数据中至少有一组数据误差小于3的概率;
参考公式:用最小二乘法求线性回归方程的系数公式:
$\stackrel{∧}{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{(\overline x)}^2}}}}$=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-}\overline y)}}{{\sum_{i=1}^n{{{(x_i^{\;}-\overline x)}^2}}}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
科研费用支出(xi)与利润(yi)统计表 单位:万元
| 年份 | 科研费用支出(xi) | 利润(yi) |
| 2011 2012 2013 2014 2015 2016 | 5 11 4 5 3 2 | 31 40 30 34 25 20 |
| 合计 | 30 | 180 |
(2)当x=xi时,由回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$得到的函数值记为$\stackrel{∧}{{y}_{i}}$,我们将ε=|$\stackrel{∧}{{y}_{i}}$-yi|称为误差;
在表中6组数据中任取两组数据,求两组数据中至少有一组数据误差小于3的概率;
参考公式:用最小二乘法求线性回归方程的系数公式:
$\stackrel{∧}{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{(\overline x)}^2}}}}$=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-}\overline y)}}{{\sum_{i=1}^n{{{(x_i^{\;}-\overline x)}^2}}}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
5.若命题:“$?{x_0}∈R,a{x^2}-ax-2>0$”为假命题,则a的取值范围是( )
| A. | (-∞,-8]∪[0,+∞) | B. | (-8,0) | C. | (-∞,0] | D. | [-8,0] |
9.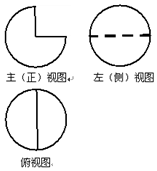 一个几何体的三视图如图所示,其中俯视图与左视图均为半径是1的圆,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中俯视图与左视图均为半径是1的圆,则这个几何体的体积是( )
 一个几何体的三视图如图所示,其中俯视图与左视图均为半径是1的圆,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中俯视图与左视图均为半径是1的圆,则这个几何体的体积是( )| A. | $\frac{4π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | π |