题目内容
若两个非零向量
与
的夹角为θ,定义
?
=|
|•|
|•sinθ,已知向量
、
满足|
|=
,|
|=4,
•
=-6,则
?
= .
| a |
| b |
| a |
| b |
| a |
| b |
| m |
| n |
| m |
| 3 |
| n |
| m |
| n |
| m |
| n |
考点:平面向量数量积的运算
专题:新定义,平面向量及应用
分析:运用向量的数量积的定义,可得cosθ,由同角的平方关系可得sinθ,再由新定义计算即可得到.
解答:
解:由于|
|=
,|
|=4,
•
=-6,
则
×4×cosθ=-6,
即有cosθ=-
,
即sinθ=
=
,
则有
?
=|
|•|
|•sinθ=
×4×
=2
.
故答案为:2
.
| m |
| 3 |
| n |
| m |
| n |
则
| 3 |
即有cosθ=-
| ||
| 2 |
即sinθ=
1-(-
|
| 1 |
| 2 |
则有
| m |
| n |
| m |
| n |
| 3 |
| 1 |
| 2 |
| 3 |
故答案为:2
| 3 |
点评:本题考查向量的数量积的定义,主要考查新定义
?
的理解和运用,属于基础题.
| a |
| b |

练习册系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积为( )


A、8+
| ||||
B、8+2
| ||||
| C、12 | ||||
D、
|
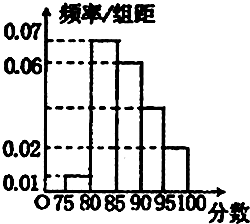 某高校在今年的自主招生考试成绩中随机抽取100名考生的笔试成绩,分为5组制出频率分布直方图如图所示.(1)求a,b,c,d;(2)该校决定在成绩较好的3,4,5组用分层抽样抽取6名学生进行面试,则每组应各抽多少名学生?
某高校在今年的自主招生考试成绩中随机抽取100名考生的笔试成绩,分为5组制出频率分布直方图如图所示.(1)求a,b,c,d;(2)该校决定在成绩较好的3,4,5组用分层抽样抽取6名学生进行面试,则每组应各抽多少名学生?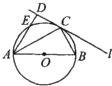 如图所示,圆O的直径AB=6.C为圆周上一点,BC=3过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于点D,E,则线段AE的长为
如图所示,圆O的直径AB=6.C为圆周上一点,BC=3过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于点D,E,则线段AE的长为