题目内容
若cos(-
+α)=
,求sin(
-α)的值.
| 14π |
| 3 |
| 1 |
| 5 |
| 13π |
| 6 |
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:由诱导公式及两角和与差的余弦函数公式化简已知可得-sin(
-α)=
,由诱导公式化简所求后即可得解.
| π |
| 6 |
| 1 |
| 5 |
解答:
解:cos(-
+α)=
,
⇒cos(
-α)=
,
⇒-
cosα+
sinα=
,
⇒-(
cosα-
sinα)=-sin(
-α)=
,
∴sin(
-α)=sin(
-α)=-
.
| 14π |
| 3 |
| 1 |
| 5 |
⇒cos(
| 2π |
| 3 |
| 1 |
| 5 |
⇒-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 5 |
⇒-(
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
| 1 |
| 5 |
∴sin(
| 13π |
| 6 |
| π |
| 6 |
| 1 |
| 5 |
点评:本题主要考察了两角和与差的正弦函数,余弦函数公式的应用,考查了诱导公式的应用,属于基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△A BC中,“
•
>0”是“△ABC为锐角三角形”的( )
| AB |
| AC |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
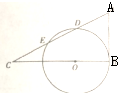 如图,圆O的圆心在Rt△ABC的直角边BC上,该圆与直角边AB相切,与斜边AC交于点D、E,AD=DE=EC,AB=
如图,圆O的圆心在Rt△ABC的直角边BC上,该圆与直角边AB相切,与斜边AC交于点D、E,AD=DE=EC,AB=
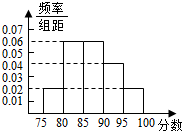 某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:
某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查: