题目内容
在△ABC中,AB=
,BC=3,AC=4,求AC边上的中线BD的长.
| 3 |
考点:正弦定理
专题:解三角形
分析:如图所示,设D为BC的中点,∠ADB=α.在△ABD与△ADC中,由余弦定理可得:AB2=AD2+BD2-2AD•BDcosα,AC2=AD2+CD2-2AD•CDcos(π-α),
相加可得:AB2+AC2=2AD2+
BC2,解出即可.
相加可得:AB2+AC2=2AD2+
| 1 |
| 2 |
解答:
解:如图所示,
设D为BC的中点,∠ADB=α.
在△ABD与△ADC中,由余弦定理可得:AB2=AD2+BD2-2AD•BDcosα,
AC2=AD2+CD2-2AD•CDcos(π-α),
相加可得:AB2+AC2=2AD2+
BC2,
即3+16=2AD2+
×9,
解得AD=
.

设D为BC的中点,∠ADB=α.
在△ABD与△ADC中,由余弦定理可得:AB2=AD2+BD2-2AD•BDcosα,
AC2=AD2+CD2-2AD•CDcos(π-α),
相加可得:AB2+AC2=2AD2+
| 1 |
| 2 |
即3+16=2AD2+
| 1 |
| 2 |
解得AD=
| ||
| 2 |
点评:本题考查了余弦定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知正项数列{an}中,a1=1,a2=2,2an2=an+12+an-12,则a6等( )
| A、16 | ||
| B、4 | ||
C、2
| ||
| D、45 |

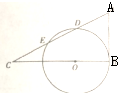 如图,圆O的圆心在Rt△ABC的直角边BC上,该圆与直角边AB相切,与斜边AC交于点D、E,AD=DE=EC,AB=
如图,圆O的圆心在Rt△ABC的直角边BC上,该圆与直角边AB相切,与斜边AC交于点D、E,AD=DE=EC,AB=