题目内容
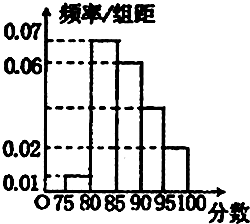某高校在今年的自主招生考试成绩中随机抽取100名考生的笔试成绩，分为5组制出频率分布直方图如图所示．（1）求a，b，c，d；（2）该校决定在成绩较好的3，4，5组用分层抽样抽取6名学生进行面试，则每组应各抽多少名学生？| 组别 | 成绩 | 人数 | 频率 |
| 1 | [75，80） | 5 | 0.05 |
| 2 | [80，85） | 35 | 0.35 |
| 3 | [85，90） | a | b |
| 4 | [90，95） | c | d |
| 5 | [95，100] | 10 | 0.1 |
考点：频率分布直方图,分层抽样方法
专题：概率与统计
分析：（1）根据频率分布表与分布直方图，求出对应的频率与频数即可；
（2）根据分层抽样方法的特点，求出每一小组应抽取的人数即可．
（2）根据分层抽样方法的特点，求出每一小组应抽取的人数即可．
解答：
解：（1）根据频率分布直方图，得；
数据在[85，90）内的频率为b=0.06×5=0.3，
对应的频数为a=100×0.3=30，
数据在[90，95）内的频率为
d=1-0.05-0.35-0.3-0.1=0.2，
对应的频数为c=100×0.2=20；
（2）3，4，5组共有30+20+10=60人，
所以第3组应抽6×
=3人，
第4组应抽6×
=2人，
第5组应抽6×
=1人．
数据在[85，90）内的频率为b=0.06×5=0.3，
对应的频数为a=100×0.3=30，
数据在[90，95）内的频率为
d=1-0.05-0.35-0.3-0.1=0.2，
对应的频数为c=100×0.2=20；
（2）3，4，5组共有30+20+10=60人，
所以第3组应抽6×
| 30 |
| 60 |
第4组应抽6×
| 20 |
| 60 |
第5组应抽6×
| 10 |
| 60 |
点评：本题考查了频率分布表与分布直方图的应用问题，也考查了分层抽样方法的应用问题，是基础题目．
练习册系列答案
相关题目
P是椭圆上的点，F1，F2是它的焦点，∠PF1F2=75°，∠PF2F1=15°，则椭圆的焦距与长轴长之比为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知抛物线C：y2=2px（p＞0）的焦点为F，A（3，t）（t＞0）为抛物线C上一点，过点A的直线l交x轴的正半轴于点D，且△ADF为正三角形，则p=（ ）
| A、2 | B、18 |
| C、2或18 | D、4或36 |