题目内容
在配置某种清洗液时,需加入某种材料.经验表明,加入量大于130mL肯定不好,用150mL的锥形量杯计量加入量,该量杯的量程分为15格,每格代表10mL,用分数法找出这种材料的最优加入量,则第一个试点应安排在 mL.
考点:分数法的应用
专题:选作题,等差数列与等比数列
分析:本题考查的知识点是优选法中的分数法:一般地,用分数法安排试点时,可以分两种情况考虑.(1)可能的试点总数正好是某一个(Fn-1).(2)所有可能的试点总数大于某一(Fn-1),而小于(Fn+1-1).这时可以用分数法解决.
解答:
解:在数列
,
,
,
,…,
中,
我们可得:F4=5,F5=8,F6=13
如下图所示:
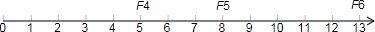
则:x1=0+
×(130-0)=80,
故答案为:80.
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 5 |
| 5 |
| 8 |
| Fn |
| Fn+1 |
我们可得:F4=5,F5=8,F6=13
如下图所示:
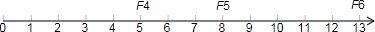
则:x1=0+
| 8 |
| 13 |
故答案为:80.
点评:分数法的适用范围:目标函数为单峰函数,可以应用于试点只能取整数值或某些特定数的情形,以及限定次数或给定精确度的问题,因为和0.618一样,这些分数都是黄金分割常数的近似值,所以对试验范围为连续的情形也可以用.

练习册系列答案
相关题目
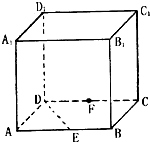 正方体ABCD-A1B1C1D1的棱长为a,E是棱AB的中点,F是棱CD的中点.
正方体ABCD-A1B1C1D1的棱长为a,E是棱AB的中点,F是棱CD的中点.