题目内容
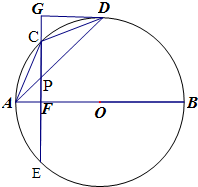 如图,AB为⊙O的直径,点D是⊙O上的一点,点C是弧AD的中点,弦CE⊥AB于F.GD是⊙O的切线,且与EC的延长线相交于点G,连接AD,交CE于点P.
如图,AB为⊙O的直径,点D是⊙O上的一点,点C是弧AD的中点,弦CE⊥AB于F.GD是⊙O的切线,且与EC的延长线相交于点G,连接AD,交CE于点P.(Ⅰ)证明:△ACD∽△APC;
(Ⅱ)若GD=
| 2 |
考点:与圆有关的比例线段
专题:选作题,立体几何
分析:(Ⅰ)证明
=
=
,可得∠ACE=∠ADC,利用∠CAP为公共角,可得△ACD∽△APC;
(Ⅱ)证明∠GED=∠ADE=∠CDA,可得∠GPD=∠GDP,所以GP=GD=
+1,利用GD2=GC•GE,求出GE,即可求PE的长.
 |
| AC |
 |
| CD |
 |
| AE |
(Ⅱ)证明∠GED=∠ADE=∠CDA,可得∠GPD=∠GDP,所以GP=GD=
| 2 |
解答:
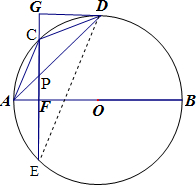 (Ⅰ)证明:∵AB为⊙O的直径,CE⊥AB,
(Ⅰ)证明:∵AB为⊙O的直径,CE⊥AB,
∴
=
∵点C是弧AD的中点,
∴
=
=
,
∴∠ACE=∠ADC,
∴∠CAP为公共角,
∴△ACD∽△APC;
(Ⅱ)解:连接DE,
∵GD是⊙O的切线,
∴∠GDX=∠CED,
∵
=
=
,
∴∠GED=∠ADE=∠CDA,
∴∠GPD=∠GDP,
∴GP=GD=
+1,
∵GD2=GC•GE,
∴GE=3+2
,
∴PE=GE-GP=2+
.
 (Ⅰ)证明:∵AB为⊙O的直径,CE⊥AB,
(Ⅰ)证明:∵AB为⊙O的直径,CE⊥AB,∴
 |
| AC |
 |
| AE |
∵点C是弧AD的中点,
∴
 |
| AC |
 |
| CD |
 |
| AE |
∴∠ACE=∠ADC,
∴∠CAP为公共角,
∴△ACD∽△APC;
(Ⅱ)解:连接DE,
∵GD是⊙O的切线,
∴∠GDX=∠CED,
∵
 |
| AC |
 |
| CD |
 |
| AE |
∴∠GED=∠ADE=∠CDA,
∴∠GPD=∠GDP,
∴GP=GD=
| 2 |
∵GD2=GC•GE,
∴GE=3+2
| 2 |
∴PE=GE-GP=2+
| 2 |
点评:此题是圆的综合题,其中涉及到切线的性质,圆周角定理,垂径定理,圆心角、弧、弦的关系定理,相似三角形的判定与性质,熟练掌握性质及定理是解决本题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
将4名实习教师分配到高一年级三个班实习,每班至少安排一名教师,则不同的分配方案有( )种.
| A、12 | B、36 | C、72 | D、108 |
