题目内容
已知{an}是等差数列，a7=12，则该数列前13项和S13等于（ ）
| A、156 | B、132 |
| C、110 | D、100 |
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：由等差数列的求和公式和性质可得S13=13a7，代值计算可得．
解答：
解：∵等差数列{an}中a7=12，
∴数列前13项和S13=
（a1+a13）=
×2a7=13a7=13×12=156
故选：A
∴数列前13项和S13=
| 13 |
| 2 |
| 13 |
| 2 |
故选：A
点评：本题考查等差数列的求和公式和性质，属基础题．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
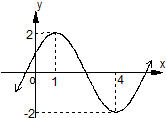已知简谐运动f（x）=Asin（ωx+φ），（|φ|＜| π |
| 2 |
则该简谐运动的最小正周期和初相φ分别为（ ）
A、T=6，φ=
| ||
B、T=6，φ=
| ||
C、T=6，φ=
| ||
D、T=6，φ=
|
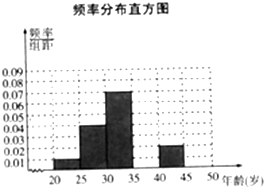为调查市民对汽车品牌的认可度，在秋季车展上，从有意购车的500名市民中，随机抽样100名市民，按年龄情况进行统计的频率分布表Ⅰ和频率分布直方图2在△ABC中，角A，B，C的对边分别为a，b，c，且b2+a2=c2+
ab，则内角C=（ ）
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f（x）是定义域为R的偶函数，当x≥0时，f（x）=x（2-x）．