题目内容
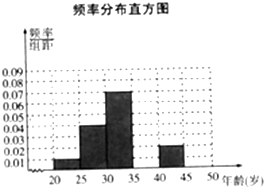 为调查市民对汽车品牌的认可度,在秋季车展上,从有意购车的500名市民中,随机抽样100名市民,按年龄情况进行统计的频率分布表Ⅰ和频率分布直方图2
为调查市民对汽车品牌的认可度,在秋季车展上,从有意购车的500名市民中,随机抽样100名市民,按年龄情况进行统计的频率分布表Ⅰ和频率分布直方图2频率分布表Ⅰ
| 分组(单位:岁) | 频数 | 频率 |
| [20,25] | 5 | 0.05 |
| [25,30] | 20 | 0.20 |
| [30,35] | ① | 0.350 |
| [35,40] | 30 | ② |
| [40,45] | 10 | 0.10 |
| 合计 | 100 | 1.000 |
(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加的宣传活动,再从这20名中选取2名志愿者担任主要发言人.记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望.
考点:离散型随机变量的期望与方差,频率分布直方图,离散型随机变量及其分布列
专题:概率与统计
分析:(1)利用频率分布表和频率分布直方图能求出频率分布表中的①②位置应填什么数,并补全频率分布直方图,再根据频率分布直方图能统计出这500名志愿者得平均年龄.
(2)由表知,抽取的20人中,年龄低于30岁的有5人,故X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列及数学期望.
(2)由表知,抽取的20人中,年龄低于30岁的有5人,故X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列及数学期望.
解答:
解:(1)由题意知频率分布表中的①位置应填数字为:
100-5-20-30-10=35,
②位置应填数字为:
=0.30.
补全频率分布直方图,
如右图所示.
平均年龄估值为:
(45×0.05+55×0.2+65×0.35+75×0.3+85×0.1)=33.5(岁).
(2)由表知,抽取的20人中,年龄低于30岁的有5人,故X的可能取值为0,1,2,
P(X=0)=
=
,
P(X=1)=
=
,
P(X=2)=
=
,
∴X的分布列为:
EX=0×
+1×
+2×
=
.

100-5-20-30-10=35,
②位置应填数字为:
| 30 |
| 100 |
补全频率分布直方图,
如右图所示.
平均年龄估值为:
| 1 |
| 2 |
(2)由表知,抽取的20人中,年龄低于30岁的有5人,故X的可能取值为0,1,2,
P(X=0)=
| ||
|
| 21 |
| 38 |
P(X=1)=
| ||||
|
| 15 |
| 38 |
P(X=2)=
| ||
|
| 1 |
| 19 |
∴X的分布列为:
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 21 |
| 38 |
| 15 |
| 38 |
| 1 |
| 19 |
| 1 |
| 2 |
点评:本题考查频率分布直方图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
已知sin2α=
,则cos2(α-
)=( )
| 1 |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知{an}是等差数列,a7=12,则该数列前13项和S13等于( )
| A、156 | B、132 |
| C、110 | D、100 |