题目内容
19.设$a=\int_0^π{sinxdx}$,则${(a\sqrt{x}+\frac{1}{x})^6}$展开式的常数项为( )| A. | -20 | B. | 20 | C. | -160 | D. | 240 |
分析 利用定积分求出a的值,再利用二项式展开式的通项公式求出展开式的常数项.
解答 解:$a=\int_0^π{sinxdx}$=-cosx${|}_{0}^{π}$=-(cosπ-cos0)=2,
则${(a\sqrt{x}+\frac{1}{x})^6}$=${(2\sqrt{x}+\frac{1}{x})}^{6}$展开式的通项公式为:
Tr+1=${C}_{6}^{r}$•${(2\sqrt{x})}^{6-r}$•${(\frac{1}{x})}^{r}$
=26-r•${x}^{3-\frac{3}{2}r}$•${C}_{6}^{r}$,
令3-$\frac{3}{2}$r=0得:r=2.
∴展开式中的常数项为24•${C}_{6}^{2}$=240.
故选:D.
点评 本题考查了定积分与二项式展开式的通项公式应用问题,是基础题.

练习册系列答案
相关题目
9.△ABC中,角A,B,C所对的边分别是a,b,c,若角A,B,C依次成等差数列,且$a=1,c=\sqrt{3}$,则S△ABC等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{3}{4}$ |
7.已知函数f(x)=sin(ωx+φ)+cos(ωx+φ)(ω>0,0<φ<π)是奇函数,直线y=$\sqrt{2}$与函数f(x)的图象的两个相邻交点的横坐标之差的绝对值为$\frac{π}{2}$,则( )
| A. | f(x)在$(0,\frac{π}{4})$上单调递减 | B. | f(x)在$(\frac{π}{8},\frac{3π}{8})$上单调递减 | ||
| C. | f(x)在$(0,\frac{π}{4})$上单调递增 | D. | f(x)在$(\frac{π}{8},\frac{3π}{8})$上单调递增 |
8.为了解本市居民的生活成本,甲、乙、内三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),甲、乙、丙所调查数据的标准差分别为x1,x2,x3,则它们的大小关系为( )
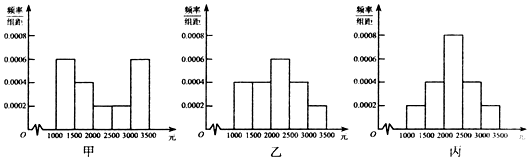

| A. | s1>s2>s3 | B. | s1>s3>s2 | C. | s3>s2>s1 | D. | s3>s1>s2 |
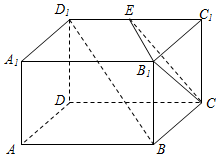 已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.
已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.