题目内容
4.如图是某企业2010年至2016年污水净化量(单位:吨)的折线图.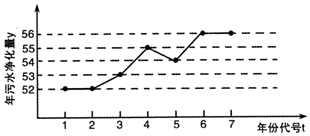
注:年份代码1~7分别对应年份2010~2016.
(1)由折线图看出,可用线性回归模型拟合y和t的关系,请用相关系数加以说明;
(2)建立y关于t的回归方程,预测2017年该企业污水净化量;
(3)请用数据说明回归方程预报的效果.
附注:参考数据:$\overline{y}$=54,$\sum_{i=1}^{7}$(ti-$\overline{t}$)(yi-$\overline{y}$)=21,$\sqrt{14}$≈3.74,$\sum_{i=1}^{7}$(yi-$\stackrel{∧}{{y}_{i}}$ )2=$\frac{9}{4}$.
参考公式:相关系数r=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$,回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{a}$+$\stackrel{∧}{b}$t中斜率和截距的最小二乘估计公式分别为$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$.
反映回归效果的公式为R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\stackrel{∧}{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$,其中R2越接近于1,表示回归的效果越好.
分析 (1)由折线图看出,y与t之间存在较强的正相关关系,将已知数据代入相关系数方程,可得答案;
(2)根据已知中的数据,求出回归系数,可得回归方程,2017年对应的t值为8,代入可预测2017年我国生活垃圾无害化处理量;
(3)求出R2,可得结论.
解答 解:(1)由题意,$\overline{t}$=4,$\sum_{i=1}^{7}$(ti-$\overline{t}$)(yi-$\overline{y}$)=21,
∴r=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$=$\frac{21}{\sqrt{28×18}}$≈0.935,
∵0.935>0.75,
故y与t之间存在较强的正相关关系;
(2)$\overline{y}$=54,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$=$\frac{21}{28}$=$\frac{3}{4}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$=54-$\frac{3}{4}×4$=51,
∴.y关于t的回归方程$\stackrel{∧}{y}$=$\frac{3}{4}$t+51,
t=8,$\stackrel{∧}{y}$=$\frac{3}{4}×8+51$=57,预测2017年该企业污水净化量约为57吨;
(3)R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\stackrel{∧}{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$=1-$\frac{1}{18}×\frac{9}{4}$≈0.875,
∴企业污水净化量的差异有87.5%是由年份引起的,这说明回归方程预报的效果是良好的.
点评 本题考查的知识点是线性回归方程,回归分析,计算量比较大,计算时要细心.

| A. | 2016 | B. | 1008 | C. | 504 | D. | 0 |
| A. | -20 | B. | 20 | C. | -160 | D. | 240 |

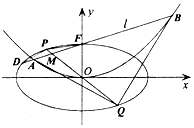 在平面直角坐标系xOy中,抛物线E:x2=4y的焦点F是椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个顶点.过点F且斜率为k(k≠0)的直线l交椭圆C于另一点D,交抛物线E于A、B两点,线段DF的中点为M,直线OM交椭圆C于P、Q两点,记直线OM的斜率为k',满足$k•k'=-\frac{1}{4}$.
在平面直角坐标系xOy中,抛物线E:x2=4y的焦点F是椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个顶点.过点F且斜率为k(k≠0)的直线l交椭圆C于另一点D,交抛物线E于A、B两点,线段DF的中点为M,直线OM交椭圆C于P、Q两点,记直线OM的斜率为k',满足$k•k'=-\frac{1}{4}$.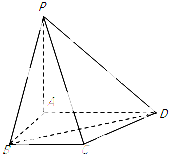 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2.求二面角A-PD-C的余弦值.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2.求二面角A-PD-C的余弦值.