题目内容
8．为了解本市居民的生活成本，甲、乙、内三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查．他们将调查所得到的数据分别绘制成频率分布直方图（如图所示），甲、乙、丙所调查数据的标准差分别为x1，x2，x3，则它们的大小关系为（ ）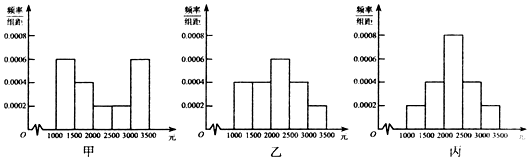
| A． | s1＞s2＞s3 | B． | s1＞s3＞s2 | C． | s3＞s2＞s1 | D． | s3＞s1＞s2 |
分析 根据题意，分析3个频率分布直方图：第二组数据是单峰的每一个小长方形的差别比较小，数字数据较分散，各个段内分布均匀，第一组数据的两端数字较多，绝大部分数字都处在两端最分散，而第三组数据绝大部分数字都在平均数左右，是集中，由此得到结果．
解答 解：根据三个频率分步直方图知，
第一组数据的两端数字较多，绝大部分数字都处在两端数据偏离平均数远，最分散，其方差、标准差最大；
第三组数据是单峰的每一个小长方形的差别比较小，数字分布均匀，数据不如第一组偏离平均数大，方差比第一组中数据中的方差、标准差小，
而第二组数据绝大部分数字都在平均数左右，数据最集中，故其方差、标准差最小，
总上可知s1＞s3＞s2，
故选：B．
点评 本题考查频率直方图的应用，涉及标准差的意义，需要从频率直方图分析波动的大小．
练习册系列答案
相关题目
18．若双曲线的焦点到渐近线的距离是焦距的$\frac{\sqrt{5}}{5}$，则该双曲线的离心率为（ ）
| A． | $\frac{2\sqrt{5}}{5}$ | B． | $\frac{\sqrt{5}}{2}$ | C． | 2 | D． | $\sqrt{5}$ |
19．设$a=\int_0^π{sinxdx}$，则${（a\sqrt{x}+\frac{1}{x}）^6}$展开式的常数项为（ ）
| A． | -20 | B． | 20 | C． | -160 | D． | 240 |
3．已知$f（x）=\left\{\begin{array}{l}a{x^2}+x，x＞0\\-x，x≤0\end{array}\right.$，若不等式f（x-1）≥f（x）对一切x∈R恒成立，则实a数的最大值为（ ）
| A． | $-\frac{9}{16}$ | B． | -1 | C． | $-\frac{1}{2}$ | D． | 1 |
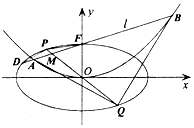在平面直角坐标系xOy中，抛物线E：x2=4y的焦点F是椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的一个顶点．过点F且斜率为k（k≠0）的直线l交椭圆C于另一点D，交抛物线E于A、B两点，线段DF的中点为M，直线OM交椭圆C于P、Q两点，记直线OM的斜率为k'，满足$k•k'=-\frac{1}{4}$．