题目内容
5.设圆x2+y2=a2与双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$1(a>0,b>0)的渐近线在第一象限的交点为M,A1,A2分别为双曲线C的左、右顶点,直线A1M交双曲线C的右支于点P,若直线A2M和A2P的倾斜角互补,则C的渐近线方程为y=x.分析 A1(-a,0),A2(a,0).联立$\left\{\begin{array}{l}{y=\frac{b}{a}x}\\{{x}^{2}+{y}^{2}={a}^{2}}\end{array}\right.$,化为(a2+b2)x2=a4,解得M$(\frac{{a}^{2}}{c},\frac{ab}{c})$.直线A1M的方程为:化为:y=$\frac{b}{a+c}$(x+a),与双曲线方程联立化为:(2ac+c2)x2-2a3x-2a4-2a3c-a2c2=0.解得P.根据直线A2M和A2P的倾斜角互补,可得${k}_{{A}_{2}P}$+${k}_{{A}_{2}M}$=0,即可得出.
解答 解:A1(-a,0),A2(a,0).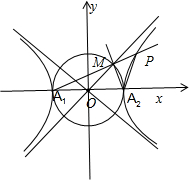
如图所示,联立$\left\{\begin{array}{l}{y=\frac{b}{a}x}\\{{x}^{2}+{y}^{2}={a}^{2}}\end{array}\right.$,化为(a2+b2)x2=a4,即c2x2=a4,x>0,
解得x=$\frac{{a}^{2}}{c}$,y=$\frac{ab}{c}$,∴M$(\frac{{a}^{2}}{c},\frac{ab}{c})$.
直线A1M的方程为:y-0=$\frac{\frac{ab}{c}-0}{\frac{{a}^{2}}{c}+a}$(x+a),化为:y=$\frac{b}{a+c}$(x+a),
联立$\left\{\begin{array}{l}{y=\frac{b}{a+c}(x+a)}\\{\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,化为:(2ac+c2)x2-2a3x-2a4-2a3c-a2c2=0.
解得x=$\frac{2{a}^{2}c+a{c}^{2}+2{a}^{3}}{2ac+{c}^{2}}$,y=$\frac{2ab(a+c)}{2ac+{c}^{2}}$.
∴P($\frac{2{a}^{2}c+a{c}^{2}+2{a}^{3}}{2ac+{c}^{2}}$,$\frac{2ab(a+c)}{2ac+{c}^{2}}$).
∴${k}_{{A}_{2}P}$=$\frac{\frac{2ab(a+c)}{2ac+{c}^{2}}}{\frac{2{a}^{2}c+a{c}^{2}+2{a}^{3}}{2ac+{c}^{2}}-a}$=$\frac{b(a+c)}{{a}^{2}}$,
又${k}_{{A}_{2}M}$=$\frac{\frac{ab}{c}-0}{\frac{{a}^{2}}{c}-a}$=$\frac{b}{a-c}$.
∵直线A2M和A2P的倾斜角互补,
∴${k}_{{A}_{2}P}$+${k}_{{A}_{2}M}$=$\frac{b(a+c)}{{a}^{2}}$+$\frac{b}{a-c}$=0,
化为:a=b.
∴C的渐近线方程为:y=x.
故答案为:y=x.
点评 本题考查了双曲线与圆的标准方程及其性质、直线与圆及其双曲线相交问题、一元二次方程的根与系数的关系、斜率计算公式,考查了推理能力与计算能力,属于难题.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
| A. | 若a>b,则ac2>bc2 | B. | 若a>b>0,则a2>b2 | ||
| C. | 若a>b,c<d,则 a-c<b-d | D. | 若a<b<0,则$\frac{1}{a}<\frac{1}{b}$ |
| A. | $\frac{4}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ | B. | $\frac{2}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ | C. | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | D. | $\frac{1}{3}\overrightarrow a+\frac{4}{3}\overrightarrow b$ |