题目内容
14.为激发学生学习兴趣,老师上课时在黑板上写出三个集合:A={x|$\frac{[]x-1}{x}$}<0,B={x|x2-3x-4≤0},C={x|log${\;}_{\frac{1}{2}}$x>2};然后请甲、乙、丙三位同学到讲台上,并将“[]”中的数告诉了他们,要求他们各用一句话来描述,以便同学们能确定该数,以下是甲、乙、丙三位同学的描述,甲:此数为小于6的正整数;乙:A是B成立的充分不必要条件;丙:A是C成立的必要不充分条件.若三位同学说的都对,则符合条件的“[]”中的数的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 先求出两个集合B,C,再根据三位同学的描述确定集合A与两个集合B,C之间的关系,推测出[]的可能取值
解答 解:由题意B={x|x2-3x-4≤0}={x|-1≤x≤4},C={x|log${\;}_{\frac{1}{2}}$x>2}={x|}{x|0<x<$\frac{1}{4}$},
A={x|$\frac{[x]-1}{x}$}<0}={x|0<x<$\frac{1}{[]}$},
由A是B成立的充分不必要条件知,A真包含于B,故$\frac{1}{[]}$≤4,再由此数为小于6的正整数得出[]≥$\frac{1}{4}$
由A是C成立的必要不充分条件得出C包含于A,故$\frac{1}{[]}$>$\frac{1}{4}$,得出[]<4,
所以[]=1,2,3.
故选:C
点评 本题考查集合中的参数取值问题,解题的关键是根据题设条件中三个同学的描述得出三个集合之间的包含关系,由这些关系得出所求的参数满足的条件,本题考查了推理论证的能力及运算能力.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
18.已知x3=4,则x等于( )
| A. | $\root{4}{3}$ | B. | $\root{3}{4}$ | C. | log34 | D. | log43 |
3.设函数f(x)=$\frac{{4}^{x}}{{4}^{x}+1}$,若[x]表示不超过x的最大整数,则函数y=[f(x)-$\frac{1}{2}$]+[f(x)+$\frac{1}{2}$]的值域是( )
| A. | {0,-1} | B. | {0,1} | C. | {-1,1} | D. | {-1,0,1} |
4.已知扇形的面积为5,周长为9,则该扇形的圆心角为( )
| A. | $\frac{5}{2}$ | B. | $\frac{8}{5}$ | C. | $\frac{5}{2}$或$\frac{8}{5}$ | D. | $\frac{5}{2}$或$\frac{4}{5}$ |
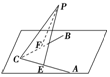 ∠ACB=90°,平面ABC外有一点P,PC=4cm,点P到角的两边AC、BC的距离都等于2$\sqrt{3}$ cm,那么PC与平面ABC所成角的大小为45°.
∠ACB=90°,平面ABC外有一点P,PC=4cm,点P到角的两边AC、BC的距离都等于2$\sqrt{3}$ cm,那么PC与平面ABC所成角的大小为45°.