题目内容
13.若对任意的实数a,函数f(x)=(x-1)lnx-ax+a+b有两个不同的零点,则实数b的取值范围是( )| A. | (-∞,-1] | B. | (-∞,0) | C. | (0,1) | D. | (0,+∞) |
分析 作出y=(x-1)lnx与y=a(x-1)-b的函数图象,根据两图象恒有两个交点得出直线定点的位置,从而得出b的范围.
解答 解:令f(x)=0得(x-1)lnx=a(x-1)-b,
令g(x)=(x-1)lnx,则g′(x)=lnx+1-$\frac{1}{x}$,
∴当0<x<1时,g′(x)<0,当x>1时,g′(x)>0,
∴g(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
作出y=(x-1)lnx与y=a(x-1)-b的大致函数图象,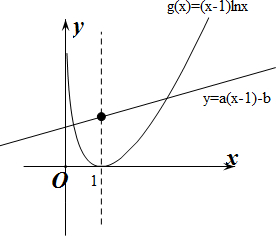
∵f(x)很有两个不同的零点,
∴y=a(x-1)-b与g(x)=(x-1)lnx恒有两个交点,
∵直线y=a(x-1)-b恒过点(1,-b),
∴-b>0,即b<0.
故选B.
点评 本题考查了函数零点与函数图象的关系,函数单调性的判断与极值计算,属于中档题.

练习册系列答案
相关题目
3.若a∈[1,6],则函数$y=\frac{{{x^2}+a}}{x}$在区间[2,+∞)内单调递增的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
4.函数y=2cos2x-sin2x的最小值是( )
| A. | -2 | B. | $1-\sqrt{2}$ | C. | $1+\sqrt{2}$ | D. | 2 |
8.边长为4的正三角形ABC中,点D在边AB上,$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{DB}$,M是BC的中点,则$\overrightarrow{AM}$•$\overrightarrow{CD}$=( )
| A. | 16 | B. | $12\sqrt{3}$ | C. | $-8\sqrt{3}$ | D. | -8 |
18.某学校门前的树上挂了两串彩灯.这两串彩灯的第一次闪亮相互独立,若都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以2秒为间隔闪亮.那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过1秒的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |