题目内容
2.已知函数f(x)=log2x,g(x)=x2,则函数y=g(f(x))-x零点的个数为3.分析 令log2x=t,将y表示为关于t的函数y=t2-2t,借助函数图象的交点个数判断.
解答 解:令f(x)=log2x=t,得x=2t,
∴y=g(f(x))-x=g(t)-2t=t2-2t,
令t2-2t=0得t=2或t=4,
作出y=t2和y=2t的函数图象,
由图象可知t2-2t=0在(-∞,0)上有一解,
故方程t2-2t=0共有3解,
又f(x)=log2x是单调函数,
∴f(x)=t有3解,
∴y=g(f(x))-x有3个零点.
故答案为3.
点评 本题考查了函数零点与函数图象的关系,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.若对任意的实数a,函数f(x)=(x-1)lnx-ax+a+b有两个不同的零点,则实数b的取值范围是( )
| A. | (-∞,-1] | B. | (-∞,0) | C. | (0,1) | D. | (0,+∞) |
10.设函数f(x)=ex(2x-3)-ax2+2ax+b,若函数 f(x)存在两个极值点x1,x2,且极小值点x1大于极大值点x2,则实数a的取值范围是( )
| A. | $({0,\frac{1}{2}})∪({2{e^{\frac{3}{2}}},+∞})$ | B. | $({-∞,\frac{1}{2}})∪({4{e^{\frac{3}{2}}},+∞})$ | C. | $({-∞,2{e^{\frac{3}{2}}}})$ | D. | $({-∞,1})∪({4{e^{\frac{3}{2}}},+∞})$ |
7.已知A,B是半径为$2\sqrt{3}$的球面上的两点,过AB作互相垂直的两个平面α、β,若α,β截该球所得的两个截面的面积之和为16π,则线段AB的长度是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
14.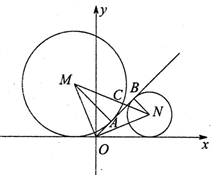 如图,圆M和圆N与直线l:y=kx分别相切于A、B,与x轴相切,并且圆心连线与l交于点C,若|OM|=|ON|且$\overrightarrow{AC}$=2$\overrightarrow{CB}$,则实数k的值为( )
如图,圆M和圆N与直线l:y=kx分别相切于A、B,与x轴相切,并且圆心连线与l交于点C,若|OM|=|ON|且$\overrightarrow{AC}$=2$\overrightarrow{CB}$,则实数k的值为( )
 如图,圆M和圆N与直线l:y=kx分别相切于A、B,与x轴相切,并且圆心连线与l交于点C,若|OM|=|ON|且$\overrightarrow{AC}$=2$\overrightarrow{CB}$,则实数k的值为( )
如图,圆M和圆N与直线l:y=kx分别相切于A、B,与x轴相切,并且圆心连线与l交于点C,若|OM|=|ON|且$\overrightarrow{AC}$=2$\overrightarrow{CB}$,则实数k的值为( )| A. | 1 | B. | $\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | $\frac{4}{3}$ |
11.已知实数$a={log_2}3{,^{\;}}b={({\frac{1}{3}})^2}{,^{\;}}c={log_{\frac{1}{3}}}\frac{1}{30}$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
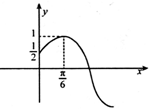 已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,0<φ<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象.
已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,0<φ<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象.