题目内容
3.若a∈[1,6],则函数$y=\frac{{{x^2}+a}}{x}$在区间[2,+∞)内单调递增的概率是( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 求出函数y=$\frac{{x}^{2}+a}{x}$在区间[2,+∞)内单调递增时,a的范围,以长度为测度,即可求出概率.
解答 解:∵函数y=$\frac{{x}^{2}+a}{x}$在区间[2,+∞)内单调递增,
∴y′=1-$\frac{a}{{x}^{2}}$=$\frac{{x}^{2}-a}{{x}^{2}}$≥0,在[2,+∞)恒成立,
∴a≤x2在[2,+∞)恒成立,
∴a≤4
∵a∈[1,6],
∴a∈[1,4],
∴函数y=$\frac{{x}^{2}+a}{x}$在区间[2,+∞)内单调递增的概率是$\frac{4-1}{6-1}$=$\frac{3}{5}$,
故选C
点评 本题考查函数的单调性,考查概率的计算,正确运用函数的单调性是关键.

练习册系列答案
相关题目
13.复数$z=|{({\sqrt{3}-i})i}|+{i^{2017}}$(i为虚数单位),则复数z的共轭复数为( )
| A. | 2-i | B. | 2+i | C. | 4-i | D. | 4+i |
14.若复数z满足$(z-1)i=\sqrt{2}$(i为虚数单位),则复数|z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{2}$ |
11.过点P(1,-3)的直线既与抛物线y=x2相切,又与圆(x-2)2+y2=5相切,则切线的斜率为( )
| A. | -6 | B. | -2 | C. | -1 | D. | 3 |
13.若对任意的实数a,函数f(x)=(x-1)lnx-ax+a+b有两个不同的零点,则实数b的取值范围是( )
| A. | (-∞,-1] | B. | (-∞,0) | C. | (0,1) | D. | (0,+∞) |
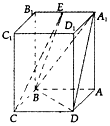 在四棱柱ABCD-A1B1C1D1中,四边形ABCD为平行四边形,AA1⊥平面ABCD,∠BAD=60°,AB=2,BC=1.AA1=$\sqrt{6}$,E为A1B1的中点.
在四棱柱ABCD-A1B1C1D1中,四边形ABCD为平行四边形,AA1⊥平面ABCD,∠BAD=60°,AB=2,BC=1.AA1=$\sqrt{6}$,E为A1B1的中点.