题目内容
8.边长为4的正三角形ABC中,点D在边AB上,$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{DB}$,M是BC的中点,则$\overrightarrow{AM}$•$\overrightarrow{CD}$=( )| A. | 16 | B. | $12\sqrt{3}$ | C. | $-8\sqrt{3}$ | D. | -8 |
分析 用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{AM},\overrightarrow{CD}$,再进行计算即可.
解答 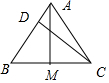 解:∵$\overrightarrow{AD}=\frac{1}{2}\overrightarrow{DB}$,∴$\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}$,
解:∵$\overrightarrow{AD}=\frac{1}{2}\overrightarrow{DB}$,∴$\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}$,
∴$\overrightarrow{CD}$=$\overrightarrow{AD}-\overrightarrow{AC}$=$\frac{1}{3}\overrightarrow{AB}$-$\overrightarrow{AC}$,
∵M是BC的中点,∴$\overrightarrow{AM}$=$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AC}$,
∴$\overrightarrow{AM}$•$\overrightarrow{CD}$=($\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AC}$)•($\frac{1}{3}\overrightarrow{AB}$-$\overrightarrow{AC}$)=$\frac{1}{6}$${\overrightarrow{AB}}^{2}$-$\frac{1}{3}$$\overrightarrow{AB}•\overrightarrow{AC}$-$\frac{1}{2}$${\overrightarrow{AC}}^{2}$,
∵三角形ABC是边长为4的正三角形,
∴${\overrightarrow{AB}}^{2}={\overrightarrow{AC}}^{2}$=16,$\overrightarrow{AB}•\overrightarrow{AC}$=4×4×cos60°=8,
∴$\frac{1}{6}$${\overrightarrow{AB}}^{2}$-$\frac{1}{3}$$\overrightarrow{AB}•\overrightarrow{AC}$-$\frac{1}{2}$${\overrightarrow{AC}}^{2}$=$\frac{8}{3}-\frac{8}{3}-8$=-8,
故选:D.
点评 本题考查了平面向量的数量积运算,属于中档题.

| A. | [3,4) | B. | (-4,-3] | C. | (1,3] | D. | [-3,-1) |
产品A产品B(其中p、q>0)
| 投资结果 | 获利40% | 不赔不赚 | 亏损20% |
| 概 率 | $\frac{1}{3}$ | $\frac{1}{2}$ | $\frac{1}{6}$ |
| 投资结果 | 获利20% | 不赔不赚 | 亏损10% |
| 概 率 | p | $\frac{1}{3}$ |
(Ⅱ)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品A和产品B之中选其一,应选用哪个?
| A. | (-∞,-1] | B. | (-∞,0) | C. | (0,1) | D. | (0,+∞) |
| A. | ω=2,φ=$\frac{π}{2}$ | B. | ω=2,φ=π | C. | ω=$\frac{1}{2}$,φ=$\frac{π}{2}$ | D. | ω=$\frac{1}{2}$,φ=$\frac{π}{4}$ |
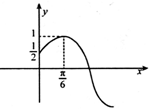 已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,0<φ<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象.
已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,0<φ<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象.