题目内容
已知定义在R上的奇函数f(x)满足f(x+2)=f(x),且当x∈(0,1)时,f(x)=tan
,则f(x)在[0,5]上的零点个数是( )
| πx |
| 2 |
| A、3 | B、4 | C、5 | D、6 |
考点:根的存在性及根的个数判断
专题:计算题,函数的性质及应用
分析:由题意可推出f(x)在[0,5]上的零点只可能在0,1,2,3,4,5这6个数中取,从而由函数的性质一一推导即可.
解答:
解:∵当x∈(0,1)时,f(x)=tan
,
∴f(x)在(0,1)上没有零点,
又∵函数f(x)是奇函数,
∴f(x)在(-1,0)上也没有零点,
又∵f(x+2)=f(x),
∴f(x)在[0,5]上的零点只可能在0,1,2,3,4,5这6个数中取,
∵f(0)=0;
故0,2,4是函数的零点,
又∵f(-1)=-f(1),f(-1)=f(1);
∴f(1)=0;
故1,3,5是函数的零点,
故f(x)在[0,5]上的零点个数是6;
故选D.
| πx |
| 2 |
∴f(x)在(0,1)上没有零点,
又∵函数f(x)是奇函数,
∴f(x)在(-1,0)上也没有零点,
又∵f(x+2)=f(x),
∴f(x)在[0,5]上的零点只可能在0,1,2,3,4,5这6个数中取,
∵f(0)=0;
故0,2,4是函数的零点,
又∵f(-1)=-f(1),f(-1)=f(1);
∴f(1)=0;
故1,3,5是函数的零点,
故f(x)在[0,5]上的零点个数是6;
故选D.
点评:本题考查了函数的零点的个数的判断,同时考查了函数的性质的综合应用,属于中档题.

练习册系列答案
相关题目
已知常数a、b、c都是实数,f(x)=ax3+bx2+cx-34的导函数为f′(x),f′(x)≤0的解集为{x|-2≤x≤3},若f(x)的极小值等于-115,则a的值是( )
A、-
| ||
B、
| ||
| C、2 | ||
| D、5 |
函数y=2-
的值域是( )
| -x2+4x |
| A、[-2,2] | ||||
| B、[1,2] | ||||
| C、[0,2] | ||||
D、[-
|
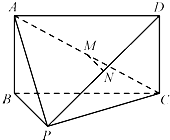 如图,在四棱锥P-ABCD中,四边形ABCD为矩形,AB⊥BP,M、N分别为AC、PD的中点.求证:
如图,在四棱锥P-ABCD中,四边形ABCD为矩形,AB⊥BP,M、N分别为AC、PD的中点.求证: