题目内容
圆M:(x-1)2+y2=9,直线l:y=x-m,当直线与圆相交于P、Q两点,若在x轴上存在一点R,使得RP⊥RQ,求M的取值范围.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:设点P、Q的坐标分别为(x1,y1),(x2,y2),R(x0,0),因为RP⊥RQ,所以(x1-x0)(x2-x0)+y1y2=0,故2x1x2-(x1+x2)(x0+m)+x02+m2=0,由圆M:(x-1)2+y2=9,直线l:y=x-m可得2x2-2(m+1)x+m2-8=0,再利用韦达定理和根与系数的关系进行求解.
解答:
解:设点P、Q的坐标分别为(x1,y1),(x2,y2),R(x0,0),
∵RP⊥RQ,
∴kRPkRQ=-1,
∴(x1-x0)(x2-x0)+y1y2=0,
∴(x1-x0)(x2-x0)+(x1-m)(x2-m)=0,
∴2x1x2-(x1+x2)(x0+m)+x02+m2=0(1)
由圆M:(x-1)2+y2=9,直线l:y=x-m可得2x2-2(m+1)x+m2-8=0
所以x1+x2=m+1,x1x2=
,
△=4(m+1)2-8(m2-8)>0,1-3
<m<1+3
将(2)代入(1)整理得x02-(m+1)x0+m2-m-8=0
所以△x0=(m+1)2-4(m2-m-8)≥0,
∴1-2
≤m≤1+2
适合△>0,
所以1-2
≤m≤1+2
.
∵RP⊥RQ,
∴kRPkRQ=-1,
∴(x1-x0)(x2-x0)+y1y2=0,
∴(x1-x0)(x2-x0)+(x1-m)(x2-m)=0,
∴2x1x2-(x1+x2)(x0+m)+x02+m2=0(1)
由圆M:(x-1)2+y2=9,直线l:y=x-m可得2x2-2(m+1)x+m2-8=0
所以x1+x2=m+1,x1x2=
| m2-8 |
| 2 |
△=4(m+1)2-8(m2-8)>0,1-3
| 2 |
| 2 |
将(2)代入(1)整理得x02-(m+1)x0+m2-m-8=0
所以△x0=(m+1)2-4(m2-m-8)≥0,
∴1-2
| 3 |
| 3 |
适合△>0,
所以1-2
| 3 |
| 3 |
点评:本题考查圆的性质和应用,考查根与系数的关系的灵活运用,考查学生的计算能力,难度中等.

练习册系列答案
相关题目
函数y=esinx(π≤x≤π)的图象大致为( )
A、 |
B、 |
C、 |
D、 |
一个几何体的三视图如图所示,则该几何体的体积、表面积为( )
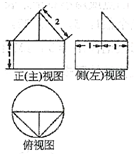

A、π+
| ||||||||
B、2π+
| ||||||||
C、π+
| ||||||||
D、2π+
|
 如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过点A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段DE的长度为
如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过点A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段DE的长度为