题目内容
已知函数f(x)=-alnx+
+x
(Ⅰ)若a>0,且曲线y=f(x)在点(1,f(1))处的切线与直线y=
x垂直,求实数a的值;
(Ⅱ)当a<0时,讨论函数f(x)的单调性;
(Ⅲ)当a∈(-∞,0)时,记函数f(x)的最小值为g(a),求证:g(a)≥-e-4.
| 2a2 |
| x |
(Ⅰ)若a>0,且曲线y=f(x)在点(1,f(1))处的切线与直线y=
| 1 |
| 2 |
(Ⅱ)当a<0时,讨论函数f(x)的单调性;
(Ⅲ)当a∈(-∞,0)时,记函数f(x)的最小值为g(a),求证:g(a)≥-e-4.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(I)f′(x)=-
-
+1,由于曲线y=f(x)在点(1,f(1))处的切线与直线y=
x垂直,可得切线在该点处的斜率k=-2.于是f′(1)=-2,又a>0,解出a即可.
(II)令f′(x)>0,f′(x)<0,解得x的范围即可得出单调区间.
(III)当a∈(-∞,0)时,由(II)可得:g(a)=-aln(-a)-3a.利用导数研究其单调性极值与最值即可得出.
| a |
| x |
| 2a2 |
| x2 |
| 1 |
| 2 |
(II)令f′(x)>0,f′(x)<0,解得x的范围即可得出单调区间.
(III)当a∈(-∞,0)时,由(II)可得:g(a)=-aln(-a)-3a.利用导数研究其单调性极值与最值即可得出.
解答:
解:(I)f′(x)=-
-
+1,
∵曲线y=f(x)在点(1,f(1))处的切线与直线y=
x垂直,
∴切线在该点处的斜率k=-2.
∴f′(1)=-a-2a2+1=-2,又a>0,
解得a=-
.
(II)f′(x)=
=
(x>0).
∵a<0,∴x-2a>0.
令f′(x)=0,解得x=-a.
令f′(x)>0,解得x>-a,此时函数f(x)单调递增;
令f′(x)<0,解得0<x<-a,此时函数f(x)单调递减.
(III)证明:当a∈(-∞,0)时,由(II)可得:g(a)=-aln(-a)-3a.
g′(a)=-ln(-a)-4,
令g′(a)=0,解得a=-e-4.
令g′(a)<0,解得a<-e-4,此时函数g(a)单调递减;令g′(a)>0,解得0<a<-e-4,此时函数g(a)单调递增.
∴g(a)≥e-4ln(e-4)+3e-4=-e-4.
| a |
| x |
| 2a2 |
| x2 |
∵曲线y=f(x)在点(1,f(1))处的切线与直线y=
| 1 |
| 2 |
∴切线在该点处的斜率k=-2.
∴f′(1)=-a-2a2+1=-2,又a>0,
解得a=-
| 3 |
| 2 |
(II)f′(x)=
| x2-ax-2a2 |
| x2 |
| (x-2a)(x+a) |
| x2 |
∵a<0,∴x-2a>0.
令f′(x)=0,解得x=-a.
令f′(x)>0,解得x>-a,此时函数f(x)单调递增;
令f′(x)<0,解得0<x<-a,此时函数f(x)单调递减.
(III)证明:当a∈(-∞,0)时,由(II)可得:g(a)=-aln(-a)-3a.
g′(a)=-ln(-a)-4,
令g′(a)=0,解得a=-e-4.
令g′(a)<0,解得a<-e-4,此时函数g(a)单调递减;令g′(a)>0,解得0<a<-e-4,此时函数g(a)单调递增.
∴g(a)≥e-4ln(e-4)+3e-4=-e-4.
点评:本题考查了利用导数研究函数的单调性、极值与最值、几何意义,考查了利用导数证明不等式,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
甲,乙,丙三名运动员在某次测试中各射击20次,三人测试成绩的频率分布条形图分别如图1,图2和图3,若S甲,S乙,S丙分别表示他们测试成绩的标准差,则( )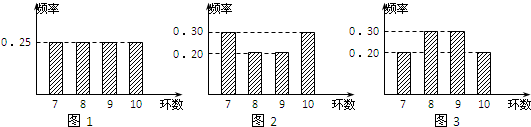

| A、S甲<S乙<S丙 |
| B、S甲<S丙<S乙, |
| C、S乙<S甲<S丙 |
| D、S丙<S甲<S乙 |
对任意x,y满足f(x+y2)=f(x)+2[f(y)]2,且f(1)≠0,则f(2013)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知随机变量X服从正态分布N(0,σ2),若P(X>2)=0.023,则P(-2≤X≤2)等于( )
| A、0.477 |
| B、0.628 |
| C、0.954 |
| D、0.977 |