题目内容
若点O和点F(2,0)分别是双曲线x2-
=1(a>0)的中心和右焦点,点P为双曲线右支上的任意一点,则
•
的取值范围为 .
| y2 |
| a2 |
| OP |
| FP |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意可求得a2=3,从而化出双曲线方程为x2-
=1,设点P(
,y),从而表达出
•
=(
,y)•(
-2,y)=1+
-2
+y2,利用换元法求值域.
| y2 |
| 3 |
1+
|
| OP |
| FP |
1+
|
1+
|
| y2 |
| 3 |
1+
|
解答:
解:由题意,1+a2=4,
解得a2=3,
则双曲线方程为x2-
=1,
∵点P为双曲线右支上的任意一点,
∴设点P(
,y),
则
•
=(
,y)•(
-2,y)
=1+
-2
+y2
令
=t,t≥1;y2=3t2-3;
故
•
=4t2-2t-3,
其在[1,+∞)上单调递增,
故
•
≥4-2-3=-1.
故答案为:-1.
解得a2=3,
则双曲线方程为x2-
| y2 |
| 3 |
∵点P为双曲线右支上的任意一点,
∴设点P(
1+
|
则
| OP |
| FP |
1+
|
1+
|
=1+
| y2 |
| 3 |
1+
|
令
1+
|
故
| OP |
| FP |
其在[1,+∞)上单调递增,
故
| OP |
| FP |
故答案为:-1.
点评:本题考查了双曲线的定义及换元法求函数的值域,属于难题.

练习册系列答案
相关题目
下面四个命题:
①分别在两个平面内的直线平行
②若两个平面平行,则其中一个平面内的任何一条直线必平行于另一个平面
③如果一个平面内的两条直线平行于另一个平面,则这两个平面平行
④如果一个平面内的任何一条直线平行于另一个平面,则这两个平面平行
其中正确的命题是( )
①分别在两个平面内的直线平行
②若两个平面平行,则其中一个平面内的任何一条直线必平行于另一个平面
③如果一个平面内的两条直线平行于另一个平面,则这两个平面平行
④如果一个平面内的任何一条直线平行于另一个平面,则这两个平面平行
其中正确的命题是( )
| A、①② | B、②④ | C、①③ | D、②③ |
甲,乙,丙三名运动员在某次测试中各射击20次,三人测试成绩的频率分布条形图分别如图1,图2和图3,若S甲,S乙,S丙分别表示他们测试成绩的标准差,则( )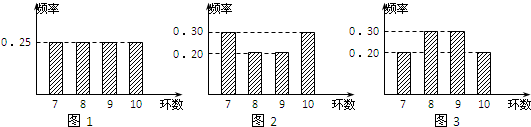

| A、S甲<S乙<S丙 |
| B、S甲<S丙<S乙, |
| C、S乙<S甲<S丙 |
| D、S丙<S甲<S乙 |