题目内容
已知函数f(x)=x2+3|x-a|(a∈R).若f(x)在[-1,1]上的最小值记为g(a).
(Ⅰ)求g(a);
(Ⅱ)证明:当x∈[-1,1]时,恒有f(x)≤g(a)+6.
(Ⅰ)求g(a);
(Ⅱ)证明:当x∈[-1,1]时,恒有f(x)≤g(a)+6.
考点:二次函数的性质
专题:函数的性质及应用
分析:(Ⅰ)讨论x取值,去掉绝对值得到f(x)=
,然后讨论a和区间[-1,1]的关系,从而找到f(x)在区间[-1,1]上的解析式,而根据解析式由二次函数的单调性即可求出函数数f(x)在[-1,1]上的最小值.
(Ⅱ)根据上一问求函数f(x)在[-1,1]上最小值的方法求出它在[-1,1]上的最大值,并证明或得出该最大值小于等于g(a)+6即可.
|
(Ⅱ)根据上一问求函数f(x)在[-1,1]上最小值的方法求出它在[-1,1]上的最大值,并证明或得出该最大值小于等于g(a)+6即可.
解答:
解:(Ⅰ)f(x)=
;
∴①若a<-1,则x∈[-1,1]时,f(x)=x2+3x-3a,该函数对称轴为x=-
;
∴该函数在[-1,1]上单调递增;
∴g(a)=f(-1)=-2-3a;
②若-1≤a≤1,则x∈[-1,a)时,f(x)=x2-3x+3a,该函数对称轴为x=
;
∴该函数在[-1,a)单调递减;
∴f(x)>f(a)=a2;
x∈[a,1]时,f(x)=x2+3x-3a;
∴该函数在[a,1]上单调递增;
∴f(x)≥f(a)=a2;
∴g(a)=a2;
③若a>1,则x∈[-1,1]时,f(x)=x2-3x+3a;
∴该函数在[-1,1]上单调递减;
∴g(a)=f(1)=-2+3a;
综上得,g(a)=
;
(Ⅱ)证明:由(Ⅰ)得,①a<-1时,f(x)≤f(1)=4-3a=g(a)+6;
②-1≤a≤1时,f(x)≤4+3a,或f(x)≤4-3a;
g(a)+6-4-3a=a2-3a+2;
∵a≤1;
∴a2-3a+2≥0;
∴g(a)+6≥4+3a;
∴f(x)≤g(a)+6;
同理,f(x)≤4-3a时,也可得到f(x)≤g(a)+6;
③a>1时,f(x)≤4+3a=g(a)+6;
综上得,当x∈[-1,1]时,恒有f(x)≤g(a)+6.
|
∴①若a<-1,则x∈[-1,1]时,f(x)=x2+3x-3a,该函数对称轴为x=-
| 3 |
| 2 |
∴该函数在[-1,1]上单调递增;
∴g(a)=f(-1)=-2-3a;
②若-1≤a≤1,则x∈[-1,a)时,f(x)=x2-3x+3a,该函数对称轴为x=
| 3 |
| 2 |
∴该函数在[-1,a)单调递减;
∴f(x)>f(a)=a2;
x∈[a,1]时,f(x)=x2+3x-3a;
∴该函数在[a,1]上单调递增;
∴f(x)≥f(a)=a2;
∴g(a)=a2;
③若a>1,则x∈[-1,1]时,f(x)=x2-3x+3a;
∴该函数在[-1,1]上单调递减;
∴g(a)=f(1)=-2+3a;
综上得,g(a)=
|
(Ⅱ)证明:由(Ⅰ)得,①a<-1时,f(x)≤f(1)=4-3a=g(a)+6;
②-1≤a≤1时,f(x)≤4+3a,或f(x)≤4-3a;
g(a)+6-4-3a=a2-3a+2;
∵a≤1;
∴a2-3a+2≥0;
∴g(a)+6≥4+3a;
∴f(x)≤g(a)+6;
同理,f(x)≤4-3a时,也可得到f(x)≤g(a)+6;
③a>1时,f(x)≤4+3a=g(a)+6;
综上得,当x∈[-1,1]时,恒有f(x)≤g(a)+6.
点评:考查处理含绝对值函数的方法:讨论x取值,去掉绝对值,以及根据二次函数的单调性求二次函数的最值,以及解决分段函数问题的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
甲,乙,丙三名运动员在某次测试中各射击20次,三人测试成绩的频率分布条形图分别如图1,图2和图3,若S甲,S乙,S丙分别表示他们测试成绩的标准差,则( )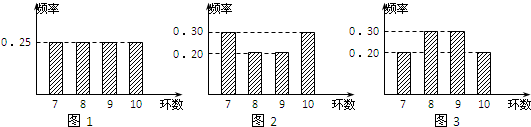

| A、S甲<S乙<S丙 |
| B、S甲<S丙<S乙, |
| C、S乙<S甲<S丙 |
| D、S丙<S甲<S乙 |
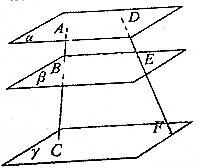 如图,直线AC、DF被三个平行平面α、β、γ所截:
如图,直线AC、DF被三个平行平面α、β、γ所截: