题目内容
函数f(x)=2x-x2在区间(0,3)上的最大值、最小值分别为( )
| A、1,-3 |
| B、0,-3 |
| C、无最大值,-3 |
| D、1,无最小值 |
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:首先写出函数的对称轴,明确区间的单调性,然后求最值.
解答:
解:因为函数f(x)=2x-x2=-(x-1)2+1,对称轴为x=1,
所以函数在(0,1)递增,在(1,3)递减,
所以函数的最大值为f(1)=2-1=1;没有最小值;
故选D.
所以函数在(0,1)递增,在(1,3)递减,
所以函数的最大值为f(1)=2-1=1;没有最小值;
故选D.
点评:本题考查了二次函数的开区间的最值求法,根据是明确对称轴与区间的位置关系,明确区间的单调性;本题注意的是区间为开区间,端点的函数值取不到,故没有最小值.

练习册系列答案
相关题目
已知a,b∈R,t>0,下列四个条件中,使a>b成立的必要不充分条件是( )
| A、a>b-t |
| B、a>b+t |
| C、|a|>|b| |
| D、4a>4b |
已知集合M={x|log3x≤1},N={x|x2-2x<0},则( )
| A、M=N | B、M∩N=∅ |
| C、M∩N=R | D、N⊆M |
正方体ABCD-A1B1C1D1中,E、F分别是AA1、AB的中点,则EF与对角面BDD1B1所成角的度数是( )
| A、30° | B、45° |
| C、60° | D、150° |
已知x+1是5和7的等差中项,则x的值为( )
| A、5 | B、6 | C、8 | D、9 |
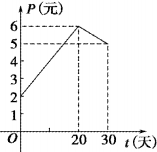 某上市股票在30填内每股交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上,该股票在30填内的日交易量Q(万股)与时间t(天)的部分数据如表所示:
某上市股票在30填内每股交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上,该股票在30填内的日交易量Q(万股)与时间t(天)的部分数据如表所示: