题目内容
设f(x)为定义在R上的偶函数,当x≥0时,f(x)=-(x-2)2+2.
(1)求函数f(x)在R上的解析式;
(2)在直角坐标系中画出函数f(x)的图象;
(3)若方程f(x)-k=0有四个解,求实数k的取值范围.
(1)求函数f(x)在R上的解析式;
(2)在直角坐标系中画出函数f(x)的图象;
(3)若方程f(x)-k=0有四个解,求实数k的取值范围.
考点:根的存在性及根的个数判断,函数奇偶性的性质
专题:数形结合,函数的性质及应用
分析:(1)令x<0,则-x>0,代入解析式,利用偶函数的性质得x<0的解析式;
(2)画出图象;
(3)结合(2),观察y=k与f(x)的图象使它们有四个交点即可.
(2)画出图象;
(3)结合(2),观察y=k与f(x)的图象使它们有四个交点即可.
解答:
解:(1)令x<0,则-x>0,所以f(-x)=-(-x-2)2+2=-(x+2)2+2.
所以函数f(x)在R上的解析式为:
f(x)=
…(4分)
(2)在直角坐标系中函数f(x)的图象如下:
 …(8分)
…(8分)
(3)结合(2)的图象,要使方程f(x)-k=0有四个解,只要y=k与f(x)的图象有四个交点,如图,
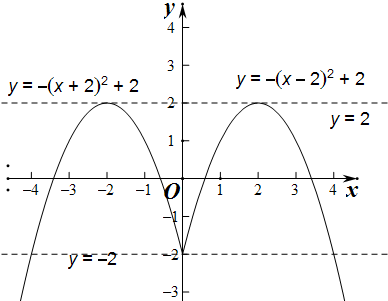
所以k的取值范围是(-2,2);…(12分)
所以函数f(x)在R上的解析式为:
f(x)=
|
(2)在直角坐标系中函数f(x)的图象如下:
 …(8分)
…(8分)(3)结合(2)的图象,要使方程f(x)-k=0有四个解,只要y=k与f(x)的图象有四个交点,如图,
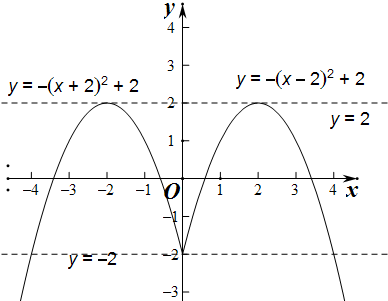
所以k的取值范围是(-2,2);…(12分)
点评:本题考查了偶函数解析式的求法以及图象的画法和利用数形结合判断方程根的个数问题,关键是正确画图、视图,属于中档题.

练习册系列答案
相关题目
已知a,b∈R,t>0,下列四个条件中,使a>b成立的必要不充分条件是( )
| A、a>b-t |
| B、a>b+t |
| C、|a|>|b| |
| D、4a>4b |
正方体ABCD-A1B1C1D1中,E、F分别是AA1、AB的中点,则EF与对角面BDD1B1所成角的度数是( )
| A、30° | B、45° |
| C、60° | D、150° |
 四边形ABCD为直角梯形,AB∥CD,AB=4,BC=CD=2,AB⊥BC,现将该梯形绕AB旋转一周形成封闭几何体,求该几何体的表面积及体积.
四边形ABCD为直角梯形,AB∥CD,AB=4,BC=CD=2,AB⊥BC,现将该梯形绕AB旋转一周形成封闭几何体,求该几何体的表面积及体积.