题目内容

在各项为正数的等比数列{an}中，若a6=a5+2a4，则公比q=
 
．
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：根据等比数列的通项公式化简a6=a5+2a4，列出关于q的方程，由各项为正数求出q的值．
解答： 解：由a6=a5+2a4得，a4q2=a4q+2a4，
即q2-q-2=0，解得q=2或q=-1，
又各项为正数，则q=2，
故答案为：2．
点评：本题考查等比数列的通项公式，注意公比的符号，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=2
3
sin（x+
π
4
）cos（x+
π
4
）-sin（2x-π）．
（1）求f（x）的单调增区间；
（2）若将函数f（x）的图象向右平移
π
3
个单位，得到函数g（x）的图象，求函数g（x）在区间[0，
π
2
]上的最大值和最小值．
正方体ABCD-A1B1C1D1中，E、F分别是AA1、AB的中点，则EF与对角面BDD1B1所成角的度数是（　　）
A、30°B、45°
C、60°D、150°
将函数y=sinx+cosx（x∈R）的图象向左平移m（m＞0）个单位长度后，得到图象关于y轴对称，则m的最小值为（　　）
A、
π
4
B、
π
3
C、
π
2
D、π
设函数f（x）=-x2+ax+3（a＞0）．
（1）求函数y=f（x）最大值；
（2）若函数在（0，3）上有零点，求实数a的取值范围；
（3）对于给定的正数a，有一个最大的正数l（a），使得在整个区间[0，l（a）]上，不等式|f（x）|≤5都成立，求l（a）表达式，并求函数l（a）最大值．
已知f（x）=
x+1，x∈[-1，0)
x2+1，x∈[0，1]
，则下列函数的图象错误的是（　　）
A、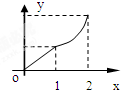
f（x-1）的图象
B、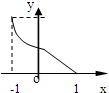
f（-x）的图象
C、
f（|x|）的图象
D、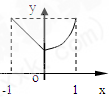
|f（x）|的图象
已知x+1是5和7的等差中项，则x的值为（　　）
A、5B、6C、8D、9
已知函数f（x）=2sinx（sinx+cosx）．
（1）求函数f（x）的最大值及相应的x值；
（2）试叙述：函数y=f（x）的图象可由函数y=sinx的图象经过怎样的变换而得到．
已知向量
m
=（-cosA，sinA），
n
=（cosB，sinB），且
m
•
n
=
2
2
，其中A，B，C分别为△ABC的三边a，b，c所对的角．
（1）求角C的大小；
（2）已知b=4，△ABC的面积为6，求边长c的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网