题目内容
已知
=(
sin2x,cos2x),
=(cos2x,-cos2x).
(Ⅰ)若当x∈(
,
)时,
•
+
=-
,求cos4x的值;
(Ⅱ)cosx≥
,x∈(0,π),若关于x的方程
•
+
=m有且仅有一个实根,求实数m的值.
| a |
| 3 |
| b |
(Ⅰ)若当x∈(
| 7π |
| 24 |
| 5π |
| 12 |
| a |
| b |
| 1 |
| 2 |
| 3 |
| 5 |
(Ⅱ)cosx≥
| 1 |
| 2 |
| a |
| b |
| 1 |
| 2 |
考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:三角函数的求值,三角函数的图像与性质,平面向量及应用
分析:(1)首先根据向量的数量积,进一步对三角函数进行恒等变换,结合题中的定义域,求出cos4x的值.
(2)根据函数的单调性和函数的交点情况,利用函数的图象求出参数m的值.
(2)根据函数的单调性和函数的交点情况,利用函数的图象求出参数m的值.
解答:
解:(1)∵已知
=(
sin2x,cos2x),
=(cos2x,-cos2x).
∴
•
+
=
sin2xcos2x-cos22x+
=
sin4x-
cos4x=sin(4x-
),
∵
•
+
=-
,
∴sin(4x-
)=-
,
∵x∈(
,
),
∴4x-
∈(π,
),
∴cos(4x-
)=-
,
∴cos4x=cos[(4x-
)+
]=cos(4x-
)cos
-sin(4x-
)sin
)=
.
(2)∵x∈(0,π),cosx在(0,π)上是单调递减函数.
∴0<x≤
令f(x)=
•
+
=sin(4x-
) g(x)=m
根据在同一坐标系中函数的图象求得:m=1或m=-
.
故答案为:
(1)cos4x=
;
(2)m=1或m=-
.
| a |
| 3 |
| b |
∴
| a |
| b |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∵
| a |
| b |
| 1 |
| 2 |
| 3 |
| 5 |
∴sin(4x-
| π |
| 6 |
| 3 |
| 5 |
∵x∈(
| 7π |
| 24 |
| 5π |
| 12 |
∴4x-
| π |
| 6 |
| 3π |
| 2 |
∴cos(4x-
| π |
| 6 |
| 4 |
| 5 |
∴cos4x=cos[(4x-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
3-4
| ||
| 10 |
(2)∵x∈(0,π),cosx在(0,π)上是单调递减函数.
∴0<x≤
| π |
| 3 |
令f(x)=
| a |
| b |
| 1 |
| 2 |
| π |
| 6 |
根据在同一坐标系中函数的图象求得:m=1或m=-
| 1 |
| 2 |
故答案为:
(1)cos4x=
3-4
| ||
| 10 |
(2)m=1或m=-
| 1 |
| 2 |
点评:本题考查的知识点:向量的数量积,三角函数式的恒等变换,三角函数的求值,函数的单调性,三角函数的图象,以及参数的取值问题.

练习册系列答案
相关题目
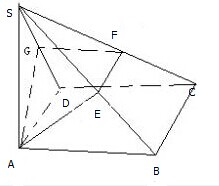 已知矩形ABCD,过A作SA⊥平面AC,再过A作AE⊥SB交SB于E,过E作EF⊥SC交SC于F.
已知矩形ABCD,过A作SA⊥平面AC,再过A作AE⊥SB交SB于E,过E作EF⊥SC交SC于F.