题目内容
(1)①证明两角和的余弦定理C(α+β)=cos(α+β)=cosαcosβ-sinαsinβ,②由C(α+β)推导两角差的正弦公式S(α-β)=sin(α-β)=sinαcosβ-cosαsinβ.
(2)已知α,β都是锐角,cosα=
,sin(α+β)=
,求sinβ.
(2)已知α,β都是锐角,cosα=
| 4 |
| 5 |
| 5 |
| 13 |
考点:两角和与差的余弦函数,两角和与差的正弦函数
专题:计算题,证明题,三角函数的求值
分析:(1)①建立单位圆,在单位圆中作出角,找出相应的单位圆上的点的坐标,由两点间距离公式建立方程化简整理即得;②由诱导公式sin(α-β)=cos[
-(α-β)]变形整理可得.
(2)由于sinβ=sin[(α+β)-α],运用公式,只要求出sinα,cos(α+β),注意角的范围,即可得到所求值.
| π |
| 2 |
(2)由于sinβ=sin[(α+β)-α],运用公式,只要求出sinα,cos(α+β),注意角的范围,即可得到所求值.
解答:
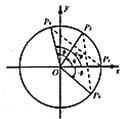 解:(1)①如图,在直角坐标系xOy内做单位圆O,
解:(1)①如图,在直角坐标系xOy内做单位圆O,
并作出角α、β与-β,使角α的始边为Ox,
交⊙O于点P1,终边交⊙O于P2;角β的始边为OP2,
终边交⊙O于P3;角-β的始边为OP1,终边交⊙O于P4.
则P1(1,0),P2(cosα,sinα)P3(cos(α+β),sin(α+β)),
P4(cos(-β),sin(-β))
由P1P3=P2P4及两点间的距离公式,得
[cos(α+β)-1]2+sin2(α+β)=[cos(-β)-cosα]2+[sin(-β)-sinα]2
展开并整理得:2-2cos(α+β)=2-2(cosαcosβ-sinαsinβ)
∴cos(α+β)=cosαcosβ-sinαsinβ;
②由①易得cos(
-α)=sinα,sin(
-α)=cosα,
sin(α-β)=cos[
-(α-β)]=cos[(
-α)+β]=cos(
-α)cosβ-sin(
-α)sinβ
=sinαcosβ-cosαsinβ;
(2)∵α是锐角,cosα=
,∴sinα=
,
∵α,β是锐角,∴π>α+β>α>0,sin(α+β)=
<sinα,∴α+β∈(
,π),
∴cos(α+β)=-
∴sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα
=
×
-(-
)×
=
.
 解:(1)①如图,在直角坐标系xOy内做单位圆O,
解:(1)①如图,在直角坐标系xOy内做单位圆O,并作出角α、β与-β,使角α的始边为Ox,
交⊙O于点P1,终边交⊙O于P2;角β的始边为OP2,
终边交⊙O于P3;角-β的始边为OP1,终边交⊙O于P4.
则P1(1,0),P2(cosα,sinα)P3(cos(α+β),sin(α+β)),
P4(cos(-β),sin(-β))
由P1P3=P2P4及两点间的距离公式,得
[cos(α+β)-1]2+sin2(α+β)=[cos(-β)-cosα]2+[sin(-β)-sinα]2
展开并整理得:2-2cos(α+β)=2-2(cosαcosβ-sinαsinβ)
∴cos(α+β)=cosαcosβ-sinαsinβ;
②由①易得cos(
| π |
| 2 |
| π |
| 2 |
sin(α-β)=cos[
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
=sinαcosβ-cosαsinβ;
(2)∵α是锐角,cosα=
| 4 |
| 5 |
| 3 |
| 5 |
∵α,β是锐角,∴π>α+β>α>0,sin(α+β)=
| 5 |
| 13 |
| π |
| 2 |
∴cos(α+β)=-
| 12 |
| 13 |
∴sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα
=
| 5 |
| 13 |
| 4 |
| 5 |
| 12 |
| 13 |
| 3 |
| 5 |
| 56 |
| 65 |
点评:本题主要考查两角和的正、余弦公式、诱导公式、同角三角函数间的关系等基础知识及运算能力.属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
 某人计划开垦一块面积为32平方米的长方形菜地,同时要求菜地周围要留出前后宽2米,左右宽1米的过道(如图),设菜地的长为x米.
某人计划开垦一块面积为32平方米的长方形菜地,同时要求菜地周围要留出前后宽2米,左右宽1米的过道(如图),设菜地的长为x米.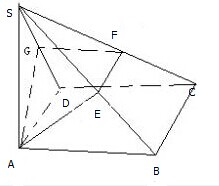 已知矩形ABCD,过A作SA⊥平面AC,再过A作AE⊥SB交SB于E,过E作EF⊥SC交SC于F.
已知矩形ABCD,过A作SA⊥平面AC,再过A作AE⊥SB交SB于E,过E作EF⊥SC交SC于F.