题目内容
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成频率分布直方图;
(2)为了能选拔出最优秀的学生,该高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求第四组至少有一名学生被考官A面试的概率?
| 成绩分组 | 频数 | 频率 |
| (160,165] | 5 | 0.05 |
| (165,170] | ① | 0.35 |
| (170,175] | 30 | ② |
| (175,180] | 20 | 0.20 |
| (180,185] | 10 | 0.10 |
| 合计 | 100 | 1 |
(2)为了能选拔出最优秀的学生,该高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求第四组至少有一名学生被考官A面试的概率?
考点:列举法计算基本事件数及事件发生的概率,频率分布表
专题:计算题,作图题,概率与统计
分析:(1)由频率=
可求其数据,频率分布直方图时注意纵轴;(2)用分层抽样的方法获取样本中的比例;(3)用古典概型求概率.
| 频数 |
| 样本容量 |
解答:
解:(1)①位置上的数据为0.35×
=35,②位置上的数据为
=0.3;
频率分布直方图如右图: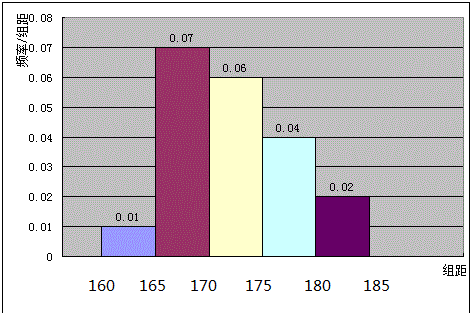
(2)6×
≈2.47,6×
≈2.11,6×
≈1.41.
故第3、4、5组每组各抽取3,2,1名学生进入第二轮面试.
(3)其概率模型为古典概型,
设第3、4、5组抽取的学生分别为:a,b,c,1,2,m.
则其所有的基本事件有:
(a,b),(a,c),(a,1),(a,2),(a,m),
(b,c),(b,1),(b,2),(b,m),
(c,1),(c,2),(c,m),
(1,2),(1,m),
(2,m).
共有15个,符合条件的有9个;
故概率为
=0.6.
| 5 |
| 0.05 |
| 30 |
| 100 |
频率分布直方图如右图:

(2)6×
| 35 |
| 35+30+20 |
| 30 |
| 85 |
| 20 |
| 85 |
故第3、4、5组每组各抽取3,2,1名学生进入第二轮面试.
(3)其概率模型为古典概型,
设第3、4、5组抽取的学生分别为:a,b,c,1,2,m.
则其所有的基本事件有:
(a,b),(a,c),(a,1),(a,2),(a,m),
(b,c),(b,1),(b,2),(b,m),
(c,1),(c,2),(c,m),
(1,2),(1,m),
(2,m).
共有15个,符合条件的有9个;
故概率为
| 9 |
| 15 |
点评:本题考查了频率分布直方图与频率分布表的作法与应用,同时考查了古典概型,属于基础题.

练习册系列答案
相关题目
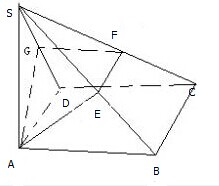 已知矩形ABCD,过A作SA⊥平面AC,再过A作AE⊥SB交SB于E,过E作EF⊥SC交SC于F.
已知矩形ABCD,过A作SA⊥平面AC,再过A作AE⊥SB交SB于E,过E作EF⊥SC交SC于F.