题目内容
已知
=(sinA,cosA),
=(
cosA,-cosA)(其中
≠
).
(1)若0<A<
,方程
•
= t-
(t∈R)有且仅有一解,求t的取值范围;
(2)设△ABC的内角A,B,C的对应边分别是a,b,c,且a=
,若
∥
,求b+c的取值范围.
| p |
| q |
| 3 |
| q |
| 0 |
(1)若0<A<
| π |
| 2 |
| p |
| q |
| 1 |
| 2 |
(2)设△ABC的内角A,B,C的对应边分别是a,b,c,且a=
| ||
| 2 |
| p |
| q |
考点:平面向量数量积的运算,平面向量共线(平行)的坐标表示
专题:平面向量及应用
分析:(1)依题意可得t=
•
+
=sin(2A-
),根据-
<2A-
<
,t=
•
+
有唯一解,可得t的范围.
(2)由
∥
(其中
≠
) 求得A=
.再根据正弦定理求得 b+c=sinB+sinC=sin(B+
) (0<B<
),结合
<B+
<
,可得b+c的取值范围.
| p |
| q |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| p |
| q |
| 1 |
| 2 |
(2)由
| p |
| q |
| q |
| 0 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
解答:
解:(1)依题意可得t=
•
+
=
sinAcosA-cos2A=
sin2A-
cos2A=sin(2A-
),
∵A∈(0,
),∴-
<2x-
<
.
再根据t=
•
+
有唯一解,可得 -
<t≤
或t=1.
(2)由
∥
(其中
≠
)得
=-1,即tanA=-
,∴A=
.
再根据正弦定理可得2R=
=1,∴b+c=sinB+sinC=sin(B+
) (0<B<
),
由
<B+
<
,可得
<b+c≤1.
| p |
| q |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∵A∈(0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
再根据t=
| p |
| q |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由
| p |
| q |
| q |
| 0 |
| sinA | ||
|
| 3 |
| 2π |
| 3 |
再根据正弦定理可得2R=
| a |
| sinA |
| π |
| 3 |
| π |
| 3 |
由
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| ||
| 2 |
点评:本题主要考查两个向量的数量积公式,正弦函数的图象特征,正弦函数的定义域和值域,正弦定理,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=2x+2x-6,用二分法求方程2x+2x-6=0在x∈(1,3)内近似解的过程中,取区间中点x0=2,那么下一个有根区间为( )
| A、(1,2) |
| B、(2,3) |
| C、(2,2.5) |
| D、(2.5,3) |
已知变量x,y,满足约束条件
,则z=3x+y的最大值为( )
|
| A、3 | ||
| B、12 | ||
C、
| ||
| D、10 |
对任意实数k,直线kx-y-3k+4=0与圆C:(x-3)2+(y-4)2=16的位置关系是( )
| A、相交 | B、相切 |
| C、相离 | D、与k取值有关 |

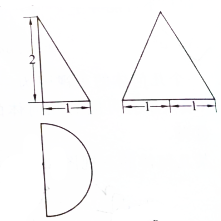 某几何体的三视图如图所示,其正视图是直角三角形,侧视图是等腰三角形,俯视图是半圆.
某几何体的三视图如图所示,其正视图是直角三角形,侧视图是等腰三角形,俯视图是半圆.