题目内容
16．设M={a，b，c}，N={-2，0，2}，从M到N的映射满足f（a）＞f（b）≥f（c），这样的映射f的个数为（ ）| A． | 1 | B． | 2 | C． | 4 | D． | 5 |
分析 由题意及映射概念逐一写出满足条件的映射得答案．
解答 解：M={a，b，c}，N={-2，0，2}，
∵f（a）＞f（b）≥f（c），
∴a对应2时，b对应0，c对应0或-2，有2个映射；
a对应2时，b对应-2，c对应-2，有1个映射；
a对应0时，b对应-2，c对应-2，有1个映射．
综上，满足条件的映射个数为4个．
故选C．
点评 本题考查映射的概念，关键是对题意及映射概念的理解，是基础题．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
7．已知$tan（θ+\frac{π}{4}）=\frac{1}{7}$且-$\frac{π}{2}$＜θ＜0，则sinθ=（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $-\frac{3}{5}$ | D． | $-\frac{4}{5}$ |
4．设min{p，q，r}为表示p，q，r三者中较小的一个，若函数f（x）=min{x+1，-2x+7，x2-x+1}，且函数f（x）的图象与直线y=m有四个交点，则m的取值范围是（ ）
| A． | [$\frac{3}{4}$，1] | B． | [$\frac{3}{4}$，1） | C． | （$\frac{3}{4}$，1] | D． | （$\frac{3}{4}$，1） |
11．如图，网格纸上小正方形边长为1，粗线是一个棱锥的三视图，则此棱锥的体积为（ ）
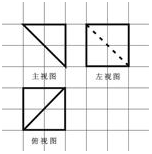
| A． | $\frac{8}{3}$ | B． | $\frac{4}{3}$ | C． | 4$\sqrt{3}$ | D． | 2$\sqrt{3}$ |
8．已知{an}是等比数列，a2=2，a5=$\frac{1}{4}$，则a1a2+a2a3+…+anan+1=（ ）
| A． | 16（1-4-n） | B． | 16（1-2-n） | C． | $\frac{32}{3}（1-{4^{-n}}）$ | D． | $\frac{32}{3}（1-{2^{-n}}）$ |
5．已知集合M={x|x2＞4}，N={-3，-2，2，3，4}，则M∩N=（ ）
| A． | {3，4} | B． | {-3，3，4} | C． | {-2，3，4} | D． | {-3，-2，2，3，4} |