题目内容
4.设min{p,q,r}为表示p,q,r三者中较小的一个,若函数f(x)=min{x+1,-2x+7,x2-x+1},且函数f(x)的图象与直线y=m有四个交点,则m的取值范围是( )| A. | [$\frac{3}{4}$,1] | B. | [$\frac{3}{4}$,1) | C. | ($\frac{3}{4}$,1] | D. | ($\frac{3}{4}$,1) |
分析 利用条件,得到函数的解析式,画出函数的图象,求解即可.
解答 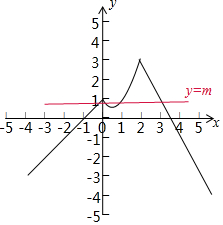 解:设min{p,q,r}为表示p,q,r三者中较小的一个,若函数f(x)=min{x+1,-2x+7,x2-x+1},
解:设min{p,q,r}为表示p,q,r三者中较小的一个,若函数f(x)=min{x+1,-2x+7,x2-x+1},
函数f(x)=$\left\{\begin{array}{l}{x+1,x≤0}\\{{x}^{2}-x+1,0<x≤2}\\{-2x+7,x>2}\end{array}\right.$,
函数的图象如图,y=x2-x+1当x=$\frac{1}{2}$时,函数取得最小值:$\frac{3}{4}$.
函数f(x)的图象与直线y=m有四个交点,
可得m∈($\frac{3}{4}$,1).
故选:D.
点评 本题考查分段函数的应用,函数的最值以及函数的零点个数的求法,考查数形结合思想以及计算能力.

练习册系列答案
相关题目
14.S=(x-1)5+5(x-1)4+10(x-1)3+10(x-1)2+5(x-1)+1,则合并同类项后S=( )
| A. | (x-2)5 | B. | (x+1)5 | ||
| C. | x5 | D. | x5+5x4+10x3+10x2+5x+1 |
19. 执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )
执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )
 执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )
执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )| A. | i≤4 | B. | i≤5 | C. | i≤6 | D. | i≤7 |
9.已知点A(a,-2),直线l的斜率为2a且过定点(0,2),B,C为直线l上的动点且|BC|=2$\sqrt{7}$,则△ABC的面积的最小值为( )
| A. | $\sqrt{7}$ | B. | 7 | C. | 2$\sqrt{7}$ | D. | 14 |