题目内容
16.已知a∈R,设函数f(x)=ax-lnx的图象在点(1,f(1))处的切线为l,则l在y轴上的截距为1.分析 求出函数的导数,然后求解切线斜率,求出切点坐标,然后求解切线方程,推出l在y轴上的截距.
解答 解:函数f(x)=ax-lnx,可得f′(x)=a-$\frac{1}{x}$,切线的斜率为:k=f′(1)=a-1,
切点坐标(1,a),切线方程l为:y-a=(a-1)(x-1),
l在y轴上的截距为:a+(a-1)(-1)=1.
故答案为:1.
点评 本题考查曲线的切线方程的求法,考查转化思想以及计算能力.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
11.有5支彩笔(除颜色外无差别),颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔,则取出的2支彩笔中含有红色彩笔的概率为( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
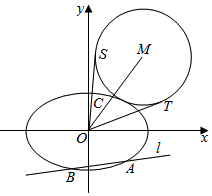 在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,焦距为2.
在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,焦距为2.